This post is an exploration of some ideas I put together for a proposed magazine article. Will link to the article if and/or when it becomes available!
Last year, I wrote a blog post about the history of “cat-turning”: the ability of cats to turn themselves over in free-fall and land on their feet. The subject has a long, long history: scientists such as James Clerk Maxwell were investigating how cats do it back in the 1850s, and a complete model of “cat-turning” did not appear until 1969, over a hundred years later!
So what intrigued and, quite frankly, baffled physicists for so long? The surprising observation is that cats can still turn over in free-fall even when they are released at rest, i.e. with no initial rotation! Ironically, this probably freaks out physicists far more than non-physicists, because at first glance it appears to be a violation of the conservation of angular momentum. In fact, when Étienne-Jules Marey first presented his photographic evidence of the phenomenon to the Paris Academy of Sciences in 1894, a number of extremely distinguished researchers argued that his claim was flat-out impossible! The cats must, they argued, push off of the hands of the person holding them at the momento f release. (Others, however, sided with Marey, and at least some of the doubters quickly changed their opinions.)

Side view of a falling cat, by Marey, c. 1894. Images chronological from right to left, top to bottom.
Fortunately, though the “complete” model of cat-turning is quite complicated, it is possible to explain the basic idea in an elegant way — without using any math! How, you may ask, can I accomplish this wizardry?
In order to understand how a cat turns over, it is best to start by explaining why simple physics gives the impression that they can’t turn over. One of the ideas that lies at the foundation of physics is the existence of conservation laws, or of physical quantities that are conserved in any closed system. Most people, for instance, are familiar with the principle of conservation of energy, which is the statement that energy cannot be created or destroyed, only changed from one form to another. An equally familiar principle is that of conservation of momentum, which states that the momentum of motion is conserved. A great illustration of this principle (via Wikipedia) is Newton’s cradle: the momentum of the ball on one side is transferred on collision to the ball on the other side. Without getting into the detailed physics, it is intuitively clear that faster objects and heavier objects have higher momentum.

Newton’s cradle animation, via Wikipedia.
A third fundamental conserved quantity is angular momentum, which we can describe as the “momentum of rotation.” Loosely speaking, we may say that an object with a high angular momentum has a high “rotational inertia,” and it is much harder to change the speed or direction of rotation. Angular momentum depends not only on the mass of an object, but also how the mass is distributed in the object, and together this resistance to rotation is called the “moment of inertia.” Given three wheels of equal mass, the wheels with larger diameter (and mass further from the axis) will have a larger moment of inertia.
This largely explains why it is easier to travel long distances by bicycle than by rollerblades: the tiny, light wheels of rollerblades lose their angular momentum due to friction much quicker than the big, heavy wheels of a bicycle.
For a rigid (i.e. non-bendy) object, the angular momentum is also proportional to the rotation rate of the object: if we double the speed of rotation (rotations/second) of a wheel, we double its angular momentum. If a wheel has no rotation, it has an angular momentum of zero.
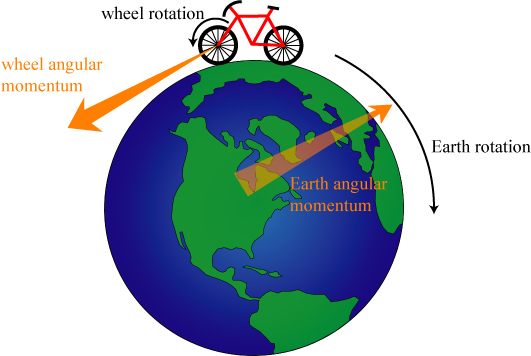
As we have said, angular momentum is a conserved quantity: in order to get an object spinning, we have to also impart equal and opposite angular momentum to something else. This leads to some pretty neat conclusions: whenever you get the wheels of your bicycle spinning, the angular momentum imparted to the wheels has been countered by an equal and opposite angular momentum imparted to the Earth itself! Thankfully, the Earth is so large and massive (i.e. has a high moment of inertia) that the actual rotation imparted to the Earth is negligible.
It should be noted in this picture that the angular momentum of the bicycle is shown as coming out of the page, whereas the angular momentum of the Earth is shown going into the page. The angular momentum of a rigid body is mathematically described as having a “direction” that is perpendicular to the plane of rotation, and follows a right-hand rule: curl the fingers of your right hand in the direction of rotation, and your thumb points in the defined direction of angular momentum. To tally the total angular momentum of a system of rotating bodies, just line the arrows of the individual objects tip to tail: the net combined arrow represents the total angular momentum. In the bicycle/Earth picture, there is no net angular momentum, as the two arrows are equal and opposite.
With this simple picture of angular momentum, it becomes clear why some scientists initially thought that it is impossible for a cat to turn over in freefall. If the cat is released without any initial rotation, so the reasoning goes, its angular momentum is zero. In freefall, there are no forces acting on the cat that can give it a net angular momentum. Since angular momentum is proportional to the rotation speed, there is no way for a cat to complete a 180 degree rotation. So their (incorrect) reasoning goes!
The flaw in their thinking is the implicit assumption that a cat is a rigid body, an assumption that is obviously false to any cat-owner! A non-rigid object, such as a cat, can move different parts of its body in different ways, and will potentially have multiple rotations associated with it.
When different parts of a non-rigid object rotate along different axes, the relationship between net angular momentum and overall rotation becomes murky, and is exploited by cats to flip over in free-fall. To see how they do it, let’s consider a simple model of a cat* consisting of two cylinders of equal size and weight, joined by muscles at the waist.
 Now let’s look at Marey’s pictures again. At position 1, while still being held, the cat has its back arched; in terms of cylinders, the cylinders are inclined at an angle with respect to each other. Then, a fascinating thing happens: the cat adjusts the bend at its waist, and at position 2, it is now bent sideways, and facing the camera!
Now let’s look at Marey’s pictures again. At position 1, while still being held, the cat has its back arched; in terms of cylinders, the cylinders are inclined at an angle with respect to each other. Then, a fascinating thing happens: the cat adjusts the bend at its waist, and at position 2, it is now bent sideways, and facing the camera!
Let’s consider this in terms of cylinders and angular momentum. For simplicity, we imagine that the two cylinders rotate at the same speed and therefore have the same angular momentum. As the cat rotates its, uh, cylinders, it starts to flip over. However, because angular momentum is conserved, there is a counter-rotation of the entire cat with equal and opposite angular momentum. As the cat rotates sections of its body, the body as a whole rotates in the other direction.
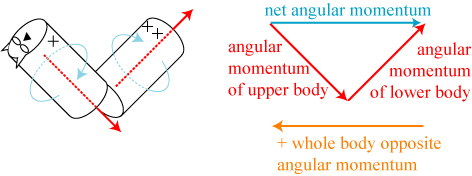 But here’s the thing: because the body is bent, the angular momenta of the upper and lower halves partially cancel out! The angular momentum of the cat as a whole, trying to rotate the cat in the other direction, is therefore less than the sum of the parts, so to speak. Also, because the cat is bent, the moment of inertia of the cat as a whole is much larger than the moments of inertia of the individual upper and lower body halves. The net result? When the cat twists, say, 270º, the whole body counter-rotation will be much less, say 90º. The net result is that the cat flips completely over, with the total angular momentum conserved and zero at all times.
But here’s the thing: because the body is bent, the angular momenta of the upper and lower halves partially cancel out! The angular momentum of the cat as a whole, trying to rotate the cat in the other direction, is therefore less than the sum of the parts, so to speak. Also, because the cat is bent, the moment of inertia of the cat as a whole is much larger than the moments of inertia of the individual upper and lower body halves. The net result? When the cat twists, say, 270º, the whole body counter-rotation will be much less, say 90º. The net result is that the cat flips completely over, with the total angular momentum conserved and zero at all times.
This simple picture of cat-turning was first advanced in 1935 by Dutch physiologists G.G.J. Rademaker and J.W.G. Ter Braak**, who performed extensive experiments with falling cats, recorded by high-speed photography.
It the diagrams above still seem a bit too complicated, we can make a remarkably elegant argument to prove that a cat must be able to turn over when bent at the waist! To do this, we consider the two most extreme cases: first, with the cat’s body completely straight, and second, with the cat’s body completely folded.
For the straight body, we break the motion into two parts for convenience. Let us imagine that the cat rotates its upper body relative to the lower body by a complete 180°. By conservation of angular momentum, the entire body counter-rotates by 90°. If the cat then tries to complete the rotation by rotating its lower body by 180°, the entire body performs another counter-rotation by 90°: the cat ends up completely upside-down again!
Now let’s imagine the cat is completely folded at the waist, and it tries the same maneuver. However, we let it rotate the upper and lower bodies at the same time, just to be efficient. If we let the upper and lower body sections rotate in the same manner as before, their rotations — and therefore their angular momentum — cancel out completely. There is no counter-rotation of the body.
Where does this leave us? There are two extremes of cat rotation. With the cat’s body straight, the 180° rotation of the body sections are completely balanced by a counter-rotation of the whole body of 180°. With the cat’s body completely folded, the rotation of the body sections come with no counter-rotation of the whole body.
What happens when the body is bent at an angle? The counter-rotation must lie somewhere between 0° and 180° — when this rotation is combined with the rotation of the body segments, we have a net rotation of the cat!
It should be noted that the Rademaker and Ter Braak model that we have presented here is oversimplified — a careful observation of actual cats turning over will show that the motion is more complicated, and likely has some variations from cat to cat. It has been noted, for example, that some (many?) cats rotate their upper body first, then their lower body. This makes practical sense, because a cat would likely want to have its paws underneath its head as fast as possible in case of a bad impact. It has also been noted that cats typically flatten their back in the final stage of flipping, in contrast to the fixed angle picture presented here. Finally, it is clear that cats use their paws to manipulate their motion, as well: by pulling its front paws in and stretching its rear paws, a cat can more quickly rotate its upper body.
It shouldn’t be surprising that cat’s motion is so complicated: evolution, unlike physics, does not have a need to produce simple, mathematically elegant solutions!
The original goal of cat-turning research was to determine how cats do it; now that this goal has been (mostly) achieved, some scientists have pointed out that cat’s ability is related to some surprisingly deep physical concepts. In particular, as noted by Robert Batterman in 2002***, cat-turning is an example of the phenomenon of geometric phase, which appears in quantum mechanics, optics, and Foucault’s pendulum!
Of these examples, Foucault’s pendulum is the easiest to explain. In 1851, French physicist Léon Foucault gave a dramatic demonstration of the rotation of the Earth by means of a large, free-hanging pendulum. After an initial demonstration at the Paris Observatory, he installed a 67 meter long pendulum at the Panthéon. The direction of oscillation of the pendulum changed by 11° every hour, completing a full circuit in 32.7 hours.

Illustration of an 1861 Foucault pendulum demonstration at the London Polytechnic Institute. Image from The World of Wonders (1883). Yes, crowds actually gathered to watch pendulums back in the day.
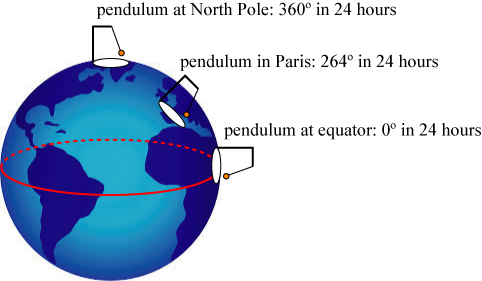
How does a pendulum demonstrate the rotation of the Earth? Put quite simply, the Earth rotates underneath the pendulum, making it appear to change direction as time passes. A pendulum on the North Pole will shift direction at 15° per hour, completing a full circuit in 24 hours. On the other hand, a pendulum on the equator will not shift direction at all. And a pendulum situated somewhere between? It will rotate somewhere between 0 and 15° per hour, depending on how close it is to the Pole. If you compare this argument to the simple discussion of cat-turning above, the parallels should be obvious!
Foucault’s pendulum and cat-turning are both physical examples where a system (the pendulum or the cat) completes a full cycle (one orbit of the Earth or a 360° flip by the cat) but ends up in a different state then it started in. In the case of the pendulum, after 24 hours it ends up swinging in a different direction than a day earlier, except at the equator or poles. In the case of the cat, after a full 360° twist of the body, the cat ends up facing in a different direction, unless it is fully bent or completely straight. This change in “state” is what is called the geometric phase.
Deeper examples of geometric phase abound. In quantum mechanics, for example, cat-turning can be connected to the Aharanov-Bohm effect, in which charged particles are affected by electric and/or magnetic fields, even though the particles never pass through those fields!
So cats can effortlessly and instinctively perform calculations that are used in extremely advanced and deep physics! Perhaps we should get a feline opinion on the most challenging physics problems of today?
***************
* Insert obligatory joke about a spherical cow here. Though, if you call feline Sabrina a cow, she will make you pay.
** G.G.J. Rademaker and J.W.G. Ter Braak, “Das Umdrehen der fallenden Katze in der Luft,” Acta oto-laryng. 23 (1935), 313-343.
*** Robert Batterman, 2002, “Falling Cats, Parallel Parking, and Polarized Light.”









The quantum connection is fascinating. Cats. Hmm. Could the quantum computing folks be barking up the wrong tree?
Heh. Probably not, but fun to think so!
per noether, it is possible or valuable to cast the question/solution in terms of space translation/galiean xform symmetries?
not galiean xform. fixed angle rotation symmetry.
I believe so, though I’d have to investigate more in order to understand the details. There’s actually a paper from early 2000s, “The gauge theory of the falling cat,” that approaches the problem in terms of symmetries!
Amazingly, this was exactly the topic discussed this week at a graduate student journal club at Johns Hopkins. https://sites.google.com/site/hardtimesjournalclub/home/schedule-spring-2014/abstracts-spring-2014/feb42014
Smarter Every Day has a fantastic illustrated video on this topic : http://www.youtube.com/watch?v=RtWbpyjJqrU
I wonder if this part ought to be tweaked:
As written, it seems to blur together the moment of inertia with the angular momentum
with the angular momentum 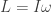 .
.