Occasionally I come across a demonstration of physics that is so simple to implement yet illustrates a phenomenon so profound that it almost takes my breath away. I learned of one such demonstration recently, which requires only a handful of readily available pieces, shown below.
 We have a helical coil of wire surrounding a steel bolt, with the wire hooked to an audio amplifier. The final piece is a moderately strong neodymium magnet.
We have a helical coil of wire surrounding a steel bolt, with the wire hooked to an audio amplifier. The final piece is a moderately strong neodymium magnet.
What can we do with this simple setup? In fact, we can do something absolutely amazing: we can hear the sound of steel being magnetized!
The phenomenon is called the Barkhausen effect, and was first reported in 1919 by the German physicist Heinrich Barkhausen (1881-1956). It was one of the first experimental glimpses into the microscopic processes that govern magnetization, and provided some of the earliest evidence for what is known as the domain theory of magnetization. In this post, we’ll look at the Barkhausen effect, what it tells us about how magnets work, and describe how you can create the effect for yourself for around $40 of readily available materials!
So what, exactly, did Barkhausen observe? With the setup above, if one brings the neodymium magnet near the wire-wrapped piece of steel, one hears a hissing noise that sounds like static or, what will turn out to be more appropriate, a rain stick.
The video below (featuring me) shows the Barkhausen effect. We observe that the hissing only appears for ferrous (iron-based) metals, i.e. metals that can be magnetized. Such materials are referred to as ferromagnetic.
To explain Barkhausen’s observation, we need to first understand a bit about magnetism, magnetic materials, and how such materials become magnetized and can stay magnetized.
If you’ve played with magnets at all, you know that they typically have a North and a South pole, and opposites attract: North poles get attracted to South, and North poles get repelled by other North poles. A magnet of this form is technically referred to as a dipole, i.e. “two poles”. This is most easy to visualize and demonstrate with a rectangular bar magnet with clearly marked N and S.
The use of the terminology “North pole” and “South pole” is not coincidental; the Earth itself, by virtue of molten iron in its outer core, acts like a gigantic bar magnet! However, what we call the magnetic North pole of the Earth is in fact the South pole of the bar magnet, to which magnetic needles (more precisely, their North poles) point.
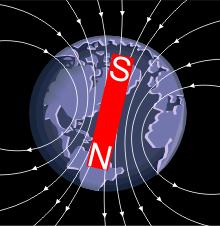
The Earth as a gigantic bar magnet. Note that magnetic North (the magnet’s South pole) is angled from the true North pole. (source)
Note the lines with arrows that pass out of the North pole of the magnet, circulate around, and reenter through the South pole. Those lines are a representation of the magnetic field produced by the Earth. In short: magnets can attract and repel each other at a distance because they produce a “force field” that extends out into space, decaying in strength further away from the magnet. We represent this force field by a set of lines with arrows. If we were to bring another bar magnet into this field, it will experience a force that tries to line it up with the lines, with the North pole pointing in the direction of the arrows. Below is a sketch of the force field of a bar magnet as drawn by me.
 This is as much as we will explain how magnets work or why magnets do what they do; beyond this simple description we would be delving into the fundamental laws of physics where “why” questions become a philosophical challenge. Instead, we will use this behavior of bar magnets as a model of all magnetic processes — with some important modifications, as we will see.
This is as much as we will explain how magnets work or why magnets do what they do; beyond this simple description we would be delving into the fundamental laws of physics where “why” questions become a philosophical challenge. Instead, we will use this behavior of bar magnets as a model of all magnetic processes — with some important modifications, as we will see.
Let us now suppose we look at the atomic structure of a piece of iron that is highly magnetized like a bar magnet. In fact, every atom of iron is inherently magnetic, and can be roughly imagined as its own tiny bar magnet! The structure of an iron bar magnet can therefore be visualized as follows.
 You might wonder how all of these little bar magnets can combine to make one big bar magnet. When the North and South poles of a pair of magnets stack together, they loosely cancel each other out; the result for our bar magnet is that the only North and South poles remaining are at the ends. This “atomic bar magnet” model of magnets also predicts that snapping a magnet in two doesn’t result in isolated North and South poles: it results in two pairs of poles.
You might wonder how all of these little bar magnets can combine to make one big bar magnet. When the North and South poles of a pair of magnets stack together, they loosely cancel each other out; the result for our bar magnet is that the only North and South poles remaining are at the ends. This “atomic bar magnet” model of magnets also predicts that snapping a magnet in two doesn’t result in isolated North and South poles: it results in two pairs of poles.
There’s something not quite right about this microscopic view of magnets, however. The pictures above show our magnetic atoms right next to each other, pointing in the same direction. But what happens if you try and put two bar magnets side by side pointing in the same direction?
Normal magnets can’t be put parallel to one another in a stable manner, but apparently “atomic magnets” can! If you suspect that quantum mechanics has something to do with it, you’re right — in ferromagnetic materials such as iron, two closely-spaced magnetic atoms minimize their so-called exchange energy by pointing in the same direction. This is such a dramatically different behavior from bar magnets that we should probably draw these atoms differently: instead of drawing them as little bar magnets, we’ll draw them as arrows pointing from the South pole to the North pole. Our completely magnetized piece of iron therefore has a new microscopic picture as follows.
Of course, this raises another question: if iron atoms like to line up in the same direction magnetically, why isn’t every piece of iron magnetized? From the naive description above, we would expect the iron to minimize its total energy by having all of its dipoles lined up in the same direction as in the picture above, and every piece of iron would therefore be a strong magnet. This doesn’t happen because there is another contribution to the energy of a piece of iron. As more and more dipoles line up pointing in the same direction, they produce a stronger and stronger magnetic field. This magnetic field energy is highest when all of the dipole are aligned in the same direction, and lowest when the dipoles are all pointing in random directions.
We therefore have two major processes in a piece of iron: the exchange force, which tries to minimize energy by making dipoles parallel, and the magnetic force, which tries to minimize energy by keeping dipoles from being parallel. In an unmagnetized piece of iron, these two forces balance out and form a compromise: they form regions in which the dipoles are all aligned, and different regions have different orientations. A non-rigorous picture of how this might play out in an unmagnetized piece of iron is shown below.
This brings us closer to understanding how the hissing sound of the Barkhausen effect is produced — if you’ve forgotten what we were trying to explain at this point!
In an unmagnetized piece of iron, the magnetic effect of all the randomly-oriented domains cancels out on average, leaving the metal with no obvious magnetic properties. If we apply an external magnetic field, however, a curious thing happens: those domains that are in line with the field grow at the expense of those that are perpendicular or opposed to the field. The picture below, again non-rigorous, gives an idea of how this might look.
The boundaries of the domains, shown as black lines in the pictures, as called domain walls. These domain walls are transition regions between the different orientations of dipoles, and when a magnetic field is applied or removed from the iron, the domain walls move.
I like to use a geopolitical analogy to explain the behaviors of these domains and domain walls! We can imagine the domains to be different countries on the map, and the domain walls the boundaries of these countries. When conditions are favorable for a particular country (an applied magnetic field points in the same direction), that country grows, engulfing its less-favored neighbors!
The domain theory of ferromagnetism was first developed in 1907 by the French physicist Pierre-Ernest Weiss, and magnetic domains are often called Weiss domains in his honor. The size and shape of domains depends strongly on the crystal structure of the magnetic material and other more subtle effects associated with it; the picture above is simply intended to convey the general idea.
If this was the entire scientific description of ferromagnetism, we would expect the magnetic properties of iron to disappear when the applied magnetic field is turned off: the dominant domain would shrink and other domains would form again, though not necessarily in their original configuration. However, if a strong enough magnetic field is applied to a piece of iron, it remains magnetized even after the field is turned off, forming a permanent magnet. How does this happen?
The answer is that no sample of iron is perfect, and inevitably contains numerous defects. These defects may be small inclusions of other materials in the iron, or may be simple imperfections in the crystal structure of iron itself. As a domain wall moves past a defect, it gets momentarily “stuck” on it: new mini domains form around the defect, creating a local minimum of energy. As the domain wall moves further along, these new domains — and the domain wall itself — are stretched further and further, creating long spikes, and at last these spikes snap free from the domain wall in a sharp atomic-scale catastrophe!

Simple illustration of the formation of spike domains. Adapted from Fig. 7.14 of the excellent text by N. Spaldin, “Magnetic Materials” (Cambridge University Press, Cambridge, 2003).
There are two important aspects to this “snapping” of a domain wall past a defect. First, it explains how iron can stay magnetized after the applied field is shut off: the domain walls try and return to their original position, but they routinely get “stuck” on a defect, leaving the metal partially magnetized. Second, this “snapping” results in a tiny spike in the magnetic field produced by the metal — and these tiny sharp changes in the magnetic field are what we are hearing in the Barkhausen effect!
How can we convert these tiny magnetic field fluctuations into sound? Our coil of wire takes advantage of Faraday induction, which I have talked about in some detail in a previous post. In short: around 1831, the brilliant experimenter Michael Faraday observed that a changing magnetic field will induce a circulating electric field, as crudely illustrated below.
Because an electric field is what drives an electrical current, a changing magnetic field in a coil of wire will induce an electrical current in that coil. The current from a tiny domain wall “snap” will be tiny, but can be enhanced with a simple audio amplifier.
In fact, it was playing around with amplifiers that led Barkhausen to his quite remarkable discovery. The English translation of his 1919 paper* is titled, “Two phenomena uncovered with the help of new amplifiers,” and the figure of his first experiment looks strikingly similar to that of my own apparatus.
Here, S represents a coil of 25mm diameter and 300 windings, G represents a galvanometer (for measuring current), V represents a 10,000 fold amplifier, and T is a telephone receiver. Barkhausen himself does not seem to have appreciated the significance of his observation, but others quickly realized its importance: the Barkhausen effect was some of the first definitive evidence in favor of the domain theory of ferromagnetism. Since that time, the phenomenon has been used to test more detailed theories about the behavior of magnetic domains as well as to understand better the internal structure of ferromagnetic materials.
So this is what you are hearing when you set up a simple Barkhausen apparatus: you are actually hearing (indirectly) the sound of metal being magnetized, in the form of atomic-level “jumps” of magnetic domain walls as they move to accommodate an applied magnetic field. I can hardly think of another circumstance where something so profound can be demonstrated so easily — and so cheaply!
One final thing: at this point, you might think that this discussion of domains and domain walls is very abstract — we’re talking about things that can’t be seen, right? On the contrary, since Barkhausen’s time a number of techniques have been developed to allow us to actually see magnetic domains through a microscope. My favorite example comes from a 1958 paper** by J.F. Dillon, Jr., “Observation of domains in the ferrimagnetic garnets by transmitted light.” Figure 4 of that paper is in my opinion both beautiful and amazing.

Reprinted with permission from J.F. Dillon, Jr., “Observation of domains in the ferrimagnetic garnets by transmitted light,” J. Appl. Phys. 29 (1958), 1286-1291. Copyright 1958, American Institute of Physics.
What we can see here is the interleaving of two domain structures in part (a), light and dark, when there is zero applied field. As the amount of field is increased (measured in Oersteds), the light domains completely overtake the dark ones. When the field is applied in the opposite direction, now the dark domains have the advantage, and as the field is made more negative they take over.
These figures were made using thin slices of garnet, a translucent ferrimagnetic material***. To observe the domains, the experimenter took advantage of another of Michael Faraday’s discoveries — Faraday rotation — in which the degree of polarization of light transmitted through a magnetic material depends significantly on the material’s magnetic state.
Want to make your own Barkhausen apparatus? It’s quite simple and inexpensive, and I explain how in the appendix to this post!
********************
* H. Barkhausen, “Zwei mit Hilfe der neuen Verstärker entdeckte Erscheinungen,” Phys. Z. 20 (1919), 401-403.
** J.F. Dillon, Jr., “Observation of domains in the ferrimagnetic garnets by transmitted light,” J. Appl. Phys. 29 (1958), 1286-1291.
*** A ferrimagnetic material is subtly different from a ferromagnetic material, though qualitatively they have similar domain behavior.
********************
APPENDIX: Make your own Barkhausen apparatus!
First I should give a shout-out to the fun and interesting website, sci-toys.com, where I first learned of the Barkhausen effect. You can purchase a Barkhausen effect kit from them for $12, minus the amplifier.
I made a slightly different setup for myself, because I wanted to be able to slip different “cores” into my coil. I designed everything to be set around 0.25” (6 mm) metal and plastic bolts, which can be purchased for roughly 25¢ each at your local hardware store. I used 2.5” long bolts. (For the steel bolt, be sure to take a magnet with you to make sure you’re buying an actual magnetic piece of steel!)
I purchased 6mm plastic tubing at my local hobby store (for a few dollars), and also bought a pair of 0.25” plastic washers to serve as the endcaps of my coil. I drilled two small holes in one of the endcaps for the magnet wire to be threaded through, and then glued the endcaps to the tube (which I cut to 2.5”), forming the coil base.
The wire for the coil is magnet wire, purchased at your local Radio Shack for about $8. I used the intermediate 26-gauge wire for my project — the 22-gauge seemed too short and the 30-gauge is too maddeningly long! You simply need to thread one end of the magnet wire through one hole in the coil base, and then get wrapping! It’s nice to try and make very regular and ordered wrappings, but in the end it doesn’t really matter if they’re neat or messy — just try and end with the other end of your wire near the other hole in the coil base.
The audio amplifier is just a Radio Shack mini audio amplifier, also available in store for $15. You need to connect the ends of your coil to a 1/8” mono plug, also available at the Shack. You’ll need a soldering iron for this, and a cheap soldering set is less than $10. Also, be sure to strip the ends of the magnet wire for a good connection — it is covered with a thin layer of enamel. I found that a hobby knife does a good job for scraping off the coating.
The only other essential piece is a strong magnet! I used a neodymium magnet, and you can get a two-pack of nice (safe) strong ones for $8.00. One more optional piece is a “soft iron” rod: “soft iron” is very pure iron that is easily magnetized and gives a very strong Barkhausen effect. You can purchase soft rods of the right diameter from a variety of sites for a few dollars.










Thanks for taking the time to write all these posts up! It’s been a great pleasure finding your blog and reading the archives.
You’re very welcome! 🙂
I have made this project on this topic as i was inspired by it and I have a question which my teacher asked me,she said,how do we know that the noise coming from the speaker is of the magnetic domains?and not something else?you know…like eddy currents?and I have a test on Wednesday based on this…so if I could get some tips,I would be thankful.Please sir,reply as soon as you can,thank you.
Short answer: I used multiple “cores” for my coil — soft iron, steel bolt, copper bolt, plastic bolt. Only the ferromagnetic ones — the iron and steel — produce the effect.
Ok sir,thanks a lot:)…could you also give me some tips as to how I should prepare to answer questions from this topic?An external will be asking us some questions based on our project,I am from India and here this effect is not known at all and plus the noise is not as good as it is in your demonstration due to the impurities in the copper wires available here.I just need some help on convincing the external,so I would be gratefull if you could help. Thanks a lot for taking out your precious time:)
No need sir,I aced my exam…but thanks for your help:)