How big is infinity? Most people, though familiar with the general concept of infinity, would probably answer with a simple, question-dodging response of “infinite.” To be fair, the infinite is a really difficult concept to wrap one’s head around, and still causes challenges and puzzles in mathematics to this day.
This is why I’m somewhat proud to have mused on some deeper issues from a very early age. When I was around 8-10 years old, I distinctly remember explaining to my mother that there had to be different sizes of infinity. My argument was as follows:
Suppose there are an infinite number of stars in the universe: that represents one size of infinity. However, every star in the universe contains a huge amount of atoms, and the total number of atoms must also be infinite. But since, for every star, there are a large number of atoms, the infinite size of the collection of atoms must be larger than the infinite size of the collection of stars.
This was surprisingly deep thinking for a pre-teen, and was at least partially right: there are different sizes to infinity. However, my argument of how to imagine different sizes of infinity was completely wrong!
To understand why, we need to talk a bit about what is known in mathematics as set theory and the properties of the smallest infinite set, which has a “size” labeled as 
Cantor circa 1870, via Wikipedia.
The ideas considered here were first discussed by the brilliant mathematician Georg Cantor (1845-1918), who between 1879 and 1884 published a series of articles introducing the mathematical foundations of set theory and discussions of infinity. So what is a set? A “set” is simply a collection of distinct objects, real or imagined, which are conceptually grouped together. The definition is incredibly broad: a group of students in a high school class forms a set (of actual objects), while the types of monsters described in the Dungeons & Dragons Monster Manual represent another set (of imagined objects).
We can also form sets out of numbers; for instance, the set e of even numbers less than ten consists of the elements:
As another example, the set p of prime numbers (which have no divisors other than themselves or one) less than 20 has the elements:
Once we have a set, we can ask how many elements it contains; this is referred to as the set’s cardinal number, or cardinality. “Cardinality” is, in effect, a fancy way of saying we are using numbers for counting things, not using numbers for ordering things (which would be an “ordinal number.”)
If we consider an infinite set, such as the natural numbers N, given by
we can no longer assign an ordinary number to describe the size of the set. However, we can compare this set to other infinite sets, and ask: which is bigger? For instance, if we consider the set of all positive even numbers E, is this set smaller than the set of natural numbers?
At first glance, we would probably say that the natural numbers are a larger set than the even numbers, just like I said that the number of atoms are greater than the number of planets, but appearances are misleading! In order to measure the size of sets properly, we need to reassess how we go about comparing large sets.
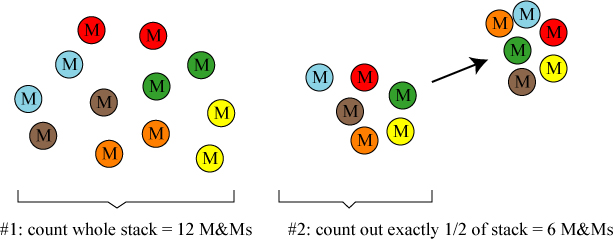
A thought experiment: suppose we have a huge bag of M&Ms (let’s assume it’s an even number, for simplicity), and we want to divide this set into a pair of piles of equal size. The most obvious solution would be to count the entire stack, and then count out exactly half of the total into a separate pile, as illustrated below.
This will of course work, but it is very inefficient: we have to count the whole stack 1 1/2 times, and there’s always the chance of a counting error along the way. If you’re dealing with someone very serious about their M&Ms, this could be a dangerous mistake!
However, there is another, faster and safer, way to count out the piles: build the two piles simultaneously, matching each M&M in one pile with a counterpart in the other. By doing so, we only have to sort through the pile one time.
This method not only saves us effort, but it doesn’t even require us to count the number of M&Ms at all: we can determine that the piles are the same size simply by putting the candy into what is called a “one-to-one correspondence.”
This same idea can be used for comparing the size of infinite sets: if every element of one set can be matched to a corresponding element of the other set, they are of the same size. Even if no ordinary number exists to describe the cardinality of an infinite set, we can discuss whether one infinite set is bigger than another.
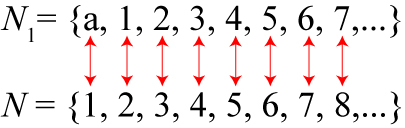
This is where things get weird! Let us do, as Cantor did, and label the cardinality of the set N of natural numbers by 
But let’s compare this set to the natural numbers! If we illustrate the effect, we have:
With that extra element added to
Or, to put it another way, “infinity plus one = infinity,” at least as far as
But this process gets even crazier! Suppose we combine a set of cardinality 
Let’s designate the elements of the first set by the natural numbers, and the elements of the second set by the primes of the natural numbers: 1′, 2′, 3′, and so forth. If we arrange the new set by putting each primed element after each unprimed element, we see that we can still put these elements into one-to-one correspondence with the natural numbers!
This means that we may also say that “infinity plus infinity equals infinity!”
DARE WE GO FURTHER!!?? YES, WE DARE! In terms of elements of the set, we may also write
as the sum of two sets of size
This process can be continued, and for any integer n, we may write
Can you see where this is going? If we take the integer n to be arbitrarily large, it seems to follow that we can write
In other words: “infinity times infinity is the same size as infinity!”
This in fact means that this AT&T commercial, with the slogan “It’s not complicated,” is even less complicated than they imagined!
How can we explain this last result? The key is to show that we can make a correspondence between an infinity-squared set of elements with the natural numbers. This is surprisingly easy to do, and in picture form, as well. Let us suppose that the natural numbers are arranged downwards vertically as an infinite set of points. Multiplying this set by infinity results in a mesh of points that stretches off infinitely to the right and downwards. But it is quite easy to draw a single line that inevitably runs through each point of this grid, as shown below.
On the left, we illustrate that we are in fact looking at infinity times infinity: the grid contains every possible pair of natural numbers. On the right, we show the beginning of the one-to-one correspondence between the natural numbers and the grid.
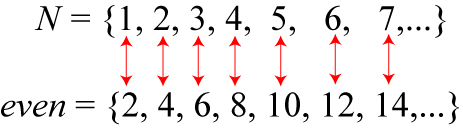
We can, in a sense, go the other way, and divide as well as multiply (though I use the term “division” loosely). For instance, we can ask: what is the size of the complete set of even numbers, which at first glance would appear to be half as numerous as the natural numbers? In fact, the cardinal number of the even numbers is still just
Most people at this point instinctively recoil from this sort of argument. “Wait,” they say. “In this correspondence, the even numbers are increasing faster than the natural numbers. We have to run out of the even numbers faster than the naturals at the end of the set — they can’t possibly be the same size!”
The short answer to this is that we never “run out” of numbers — the set is infinite! This response also feels unsatisfying. A better answer is to reverse our thinking about the one-to-one correspondence. Suppose we imagine any natural number, as large as we like, for example 100-billion-billion. We can always easily figure out the even number that is in correspondence with it, in this example 200-billion-billion. For any natural number we choose, we can find the even number that corresponds to it. By our reckoning, the two sets are therefore the same size.
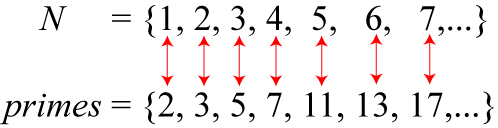
A similar argument applies to the size of the set of prime numbers. Though the prime numbers are less and less frequent in the set of natural numbers the higher we go, we can still make a one-to-one correspondence with the natural numbers. We’ve known since the time of Euclid that the number of prime numbers is infinite — since they also can be arrange in order on a number line, we can set up a one-to-one correspondence. The set of prime numbers also has cardinality
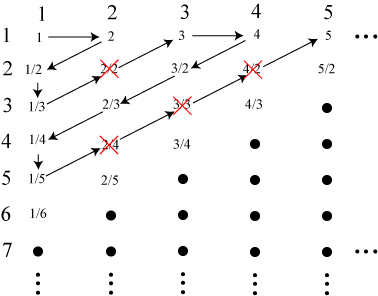
There’s one more remarkable result to share. There’s another set that is seemingly larger than the natural numbers: the set of all rational numbers. A rational number is one that can be expressed as a fraction with whole numbers, such as 1/2, 2/3, 51/100, 32/67, and so forth. This includes the entire set of natural numbers, because each natural number can be written as a fraction: 5 = 5/1, 15 = 15/1, and so on.
We might think that this set is larger than
Some elements, crossed out in red, are redundant — 2/2 is the same as 1 — and we just skip over them in our correspondence. In the end, though, we find that the entire set of rational numbers does in fact have the same cardinality as the natural numbers:
The rational numbers include the natural numbers plus a large number of fractional numbers that lie between them on the number line. We can uncover an even more surprising result and demonstrate that the set of algebraic numbers have cardinality
An algebraic number is a number that is a root of an algebraic equation of the general form
where n is any natural number and the coefficients 
So, infinity is weird! If this were the end of the story, it would be anti-climactic, and arguably not even mathematics. If all infinite sets were the same size, there would really be nothing interesting to be said about them. However, it can be shown that there are in fact infinities that are bigger than
… but that will be a discussion for the next post in this series!
(Part 2 can be read here.)
Skulls in the Stars 
Ok, maybe you can help me with this question I raised on facebook recently: Does the song “\aleph_1 Bottles of Beer On The Wall” have more verses than the song “\aleph_0 Bottles of Beer On The Wall”? I was trying arguing that both songs have \aleph_0 verses (verse 1, verse 2, verse 3 …) but some mathematician friends were getting themselves in knots about the Axiom of Choice so I gave up. What do you say?
Interesting question. It seems clear to me that the singing (or enumerating) of verses limits one to \aleph_0 verses. I suppose that one could argue that verses exist that can never be listed or sung (even if every subatomic particle in the observable universe sang its own verses for eternity).
That would be my take, as well. If you’re talking about actually ‘counting’ verses, by definition the only infinite countable set of verses would be aleph_0. aleph_1 would be the paradoxical situation where you have verses that could never be sung.
Very sweet. Thanks for this one, mathematics and set theory explained through its history.
Am I getting this right? You are suggesting that as long as we can prove a one to one representation one can argue that the infinities represented are of a equivalent amount? Now that makes sense to me considering what infinity might mean, as it being ‘no end’ to it. But isn’t it is also so that inside any defined system, we will find more natural numbers than primes describing it, for example counting atoms in a needles head? To define those atoms through primes is a possibility though? But it doesn’t feel natural to me?
Or am I getting this up side down?
Probably I am 🙂
For any finite set of natural numbers, we can always talk about there being more integers than primes, as the primes are clearly less “dense” than the naturals on the number line. When we talk about the *complete* set, however, both the naturals and the primes are a “countable” infinity, which means that they are, by the only reasonable measure (1-1 correspondence), the same size.
more clearly: one-to-one correspondence is what “same number as” JUST MEANS.
it’s not a fact, it’s the very DEFINITION of “same number as”
Set theory (particularly if one is talking about infinite sets) requires great care in the use of words and definitions. If by “defined system” you mean “finite system”, then we’re out of the realm of the infinite and things behave “normally”. In a finite set of atoms, you can certainly label them with “1, 2, 3, 4, …” or “2, 3, 5, 7, …” or any other sufficiently large set of labels.
note that you don’t have infinite NUMBERS until you have a concept of greater than and less then. and you don’t have a concept of greater/less than until you have the shroeder-bernstein theorem. and it takes a fair bit of machinery coupled with a non-obvious proof to get that.
see the halmos classic for details.
Yeah, I’m skimming over lots of the subtlety in these posts to get at the basic weirdness of concepts of infinity. More or less following some of Cantor’s original arguments!
heh cantor himself only waved his hands at the need for shroeder-bernstein.
note too that a0 + a0 = a0 and similar requires some form of AC.
for more infinity weirdness, consider the skolem “paradox”. also the famous a1 < 2^a0 question . 🙂
Then using a one to one correspondence to prove a infinity hangs on ones definition of what a infinity is, right? So, what exactly is a infinity, and can you really have lesser and greater infinities? Using a one to one correspondence all infinities should become the same, as it seems to me? It shouldn’t matter if I use primes or natural numbers for it, as long as there is no end to the correspondence?
As long as there is a one-to-one correspondence that pairs each element from Set 1 with each element from Set 2, then the sets have the same cardinality (the same number of elements). A non-empty finite set can be put in 1-1 correspondence with {1, 2, …, n} for some n. (In that case, we say that the cardinality is n.)
A set that is not finite is infinite. Here’s the fun part. Though the number of integers is the same infinity as the number of primes and is the same infinity as the number of rational numbers, the number of real numbers is a LARGER infinity. There is no 1-1 correspondence between the integers and the reals. We say that the integers are countably infinite and the reals are uncountably infinite. (See for example here:
http://mathworld.wolfram.com/CantorDiagonalMethod.html )
Keep in mind that this is a purely mathematical discussion and it there is a minimum meaningful size in the universe (like the Planck scale you mention in your other reply), and if we call pieces of the universe of this size “points” then even if the universe is infinite in extent, there are only a countably infinite number of such locations.
Yes, the cardinality of the continuum is the next blog post topic! 🙂
As a very weird example, you magnify something. Will there be a end to it? Magnification will break down around Planck scale, so? Does that mean that it ends there? In my imagination it either seems as if that should be a end, or as if our measurements fail. The point:) may be the question if you would consider that points magnification to be ‘infinite’, or ‘finite’, here?
I see that all infinites are the same size until I posit that mathematics is not itself infinite….I say that even the concept of numbers had a beginning, and before that there was a numberless void consisting of logic, from which mathematics, and the manipulation of numbers, or information, was developed from…this indicates a beginning that began a calculation algorithm based upon a conceptual precept given by said logic, that delivered a starting point with no end point(yet), as the algorithm delivers and an increasing complexity as there are continually more numbers available for the algorithm to “work with”. I see the starting number as “one” as there was “one void” within which was a dimensionless imaginary point, the geometry of any point, even an imaginary one, having a diameter to circumference ratio of PI, as it’s starting generator of information….3.14159…..and counting (I admit to the platonism of this concept).Further, I posit that the algorithm continues as we speak, adding new information to the universe and new forms of mathematics, (ala kurt godel). So, to say that there are an infinite number of anything is an untestable and redundant statement, as all the number manipulations, or information, is yet to be available A steady count of the simplest of manipulations (addition) is still adding up the talley. I further posit that there is a fundamental fastest speed to any calculation possible in this universe, given the logic structure that underpins it. That fundamental is the base rate of calcuation that generates all other fundamental constants, and supports the expression of physical reality as we observe it now. This fundamental speed of calculation is not infinte, or the calculation would have ended as soon as it started….poof…and hence no time. The slowness of the fundamental base rate or “clock frequency” of this universe allows plenty of time for things to get interesting …..but since I believe there are no infinites in the universe, eventually the algorithm PI will come out even or with a unchanging simple remainder, allowing no new information to be added to the mathematical information entireity…that could spell trouble….edd
Just a minor point: “infinity plus infinity equals infinity!” (and particularly the line below with the Aleph signs) does look rather like you are talking about “infinity factorial”…while the result is likely the same, it confused me for a moment until I realised that the exclamation mark was in fact just an exclamation mark!
Ha — good point! I’ve changed it to a less misleading period. 🙂
A doubt: \aleph_0 + \aleph_0 = (\aleph_0).2 > (\aleph_0)
2.(\aleph_0) = \aleph_0, but (\aleph_0).2 > (\aleph_0)
This is due to the fact that ordinal sum and product are non-commutative.
We’re not dealing with ordinality at all here, just cardinality. In unordered sets, a0+a0=a0.
It is not true that:
\aleph_0 + \aleph_0 > \aleph_0
Equality here means precisely “can be put in 1-1 correspondence with each other”
Teh crazies take on set theory: http://boingboing.net/2012/08/07/what-do-christian-fundamentali.html
*Sigh* There isn’t any important result in math or science that a fundie somewhere hasn’t had an issue with!