To conclude my discussion of optics basics, I want to introduce some of the standard quantities used to describe waves and wave propagation. Unlike previous ‘basics’ posts, this one will necessarily deal with a little bit of algebra and perhaps a little trigonometry.

The simplest wave to deal with from a theoretical point of view is a harmonic wave, one which consists of an infinite sequence of regularly spaced ‘ups and downs’. A portion of such a wave traveling to the right on an extremely long string would appear as:

There are a number of important properties of this wave that can be measured, the most obvious being the speed of the wave. Keeping our eyes on one of the peaks of the wave, we can measure its speed by seeing how far it goes in a certain time interval. Then we can use the simple formula:

speed = distance/time

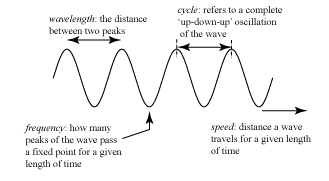
We can also measure, at a single instant of time, the distance between two peaks of the wave. This quantity is known as the wavelength, and represents the length of a single ‘up-down-up’ cycle of the wave. Finally, we can focus on one location on the wave, and measure how many cycles of the wave go by in a fixed interval of time, i.e. # cycles/time. This quantity is known as the frequency of the wave, and represents how frequently the wave repeats itself.

Looking at a snapshot of our wave, we illustrate how to measure all three quantities, and what we mean by a cycle:

In formulas, the speed of a wave is typically denoted by v (c for the speed of light), frequency is denoted by the Greek letter ν (‘nu’), and wavelength by the Greek letter λ (‘lambda’). We may also define two other related quantities, the wavenumber k = 2π/λ and angular frequency ω=2πν. Mathematically, we may write the expression for our harmonic wave as:

Here U(x,t) represents the amplitude (height) of the wave, x represents the spatial position on the wave, and t represents the time at which it is measured. ‘Sin’ is simply the trigonometric sine function. With a little bit of equation juggling, we can show that the frequency, wavelength, and speed of a wave are related. Thus:

Looking at the term in the parenthesis, a little thought shows that the speed of the wave is necessarily v = νλ. Thus frequency and wavelength are not independent quantities, but are related through the speed of the wave.

The speed (velocity) of a wave is dependent on the type of wave (sound, water, light) and the properties of the medium the wave is passing through. Light in a vacuum has a speed of roughly 300000000 meters/second. Sound waves in air have a speed of about v = 344 meters/second, but this can change significantly depending on temperature and other factors.

The individual ‘ups and downs’ of visible light is not something that we can detect directly with our eyes, or even with sophisticated sensors: the frequency is on the order of 10^15 cycles/second (a ‘1’ with fifteen zeros after it). Similarly, audible sound has frequencies ranging from 20 cycles/second to 20000 cycles/second, also resulting in ‘ups and downs’ than we can detect directly with our ears. Of course, our eyes can detect indirectly the frequency of light, which roughly translates into the color of the light.

A perfect harmonic wave, which oscillates up and down with the same frequency and wavelength for all time, is obviously a mathematical idealization. Can we assign a frequency and wavelength for an arbitrary wave disturbance, such as the one shown in the figure below?

In general, we can! It is to be noted in the figure above that the ‘ups and downs’ of the disturbance are still more or less evenly spaced, which implies a relatively well-defined wavelength. In general, we can express any wave disturbance as a sum of harmonic waves of different frequencies, and the dominant harmonic wave in that sum is the center frequency of the disturbance. Because of the simple relationship between frequency and wavelength, we can also refer to a central wavelength of the disturbance. The mathematical formalism for describing an arbitrary function or waveform as a sum of harmonic waves is known as Fourier analysis, a topic too advanced for a basics post such as this one!

There’s a lot more one can say, even on a basic level, about waves and wave behavior. In my ‘What is a wave?’ series of posts, however, I’ve attempted to single out the most important concepts and definitions which will appear in later posts on more specific and complicated topics. Time will tell if I’ve been complete enough…