I’m planning to do a long-term series of posts on Einstein’s relativity, starting with the special theory and progressing to the general theory (if you don’t know what the difference is, that’s okay, ’cause I’m gonna explain it all, eventually).
Einstein’s theories of relativity are certainly the among most elegant of all of physics. Incredibly deep and counterintuitive consequences can be derived from the statement of a small number of simple postulates, and general features of the special theory of relativity are accessible to anyone who has some familiarity with algebraic manipulation.
But no theory is created ‘in a vacuum’ (pun intended), and Einstein’s is no exception. Relativity has its roots in the very beginnings of what we now call physics, so we begin our discussion with a short introduction to the events and observations that led up to Einstein’s magnificent theories. This post will be pretty much bereft of math; later posts will include algebraic operations as needed.
The foundations of relativity were set by Galileo Galilei (1564-1642) in the 16th century. Galileo, pictured below, was an Italian scientist/philosopher who is generally credited with giving birth to modern physics.

Among his many contributions, Galileo was a master astronomer, and produced some of the best telescopes of his age. With these telescopes he made many important discoveries, including the first observations of Jupiter’s four largest moons, the rings of Saturn, and lunar mountains and craters. A number of his discoveries lent support to a heliocentric (Sun-centered) model of the solar system, and Galileo became an ardent supporter of this model.
At the time, however, scientific consensus and Church doctrine proclaimed that the Earth was the center of the universe, and that the planets, Sun and stars rotated about it on ‘celestial spheres’. This system, referred to as geocentrism, was championed by Aristotle in 5th century B.C. Greece and the astronomer Ptolemy in 2nd century B.C. Egypt. The first major challenge to this system came about in 1543 with the publication of Nicolaus Copernicus‘ book On the Revolutions of the Heavenly Spheres. Copernicus argued, and backed up with observations, that the Sun was the actual center of the solar system (heliocentrism).
A number of arguments were made against this Copernican system. One of the most powerful, at least at the time, was that if the Earth was in fact moving, we should be able to ‘feel’ the effects of this motion. Contemporary opponents of Galileo and Copernicus would argue that, if the Earth is spinning on its axis, a cannonball dropped from a tower should land some distance to the west, since the Earth would have moved some distance to the east as the cannonball fell. Similarly, you should be able to throw a ball farther to the west than to the east, since the ground is ‘moving towards’ the ball in the first case, and ‘moving away’ from the ball in the second. This argument is based on Aristotle’s flawed idea that the natural state of an object is to come to some sort of ‘absolute rest,’ i.e. an object put into motion will inevitably slow down and stop moving.
Such an idea seems reasonable in our everyday perceptions of the world. If you roll a ball along the ground, it will gradually come to a stop. If you take your foot off the gas pedal in a car, the car will gradually slow down and stop. We understand today that this slowing down occurs because of frictional forces between the car and ground and wind resistance between the car and the air, but to the early scientists it seemed eminently reasonable that the natural state of things is to remain motionless. From that viewpoint, one would expect that all things would be naturally dragged to the west if the Earth was in fact in motion.
Galileo refutes this argument and numerous others in his book Dialogue Concerning the Two Chief World Systems, in which he compares the Copernican and Ptolemic cosmologies. The text is written in the form of a dialogue between three men: Salviati (pro-Copernican), Sagredo (initially neutral), and Simplicio (pro-Ptolemic). In response to the arguments stated above, Salviati presents the following ‘thought experiment’:
Shut yourself up with some friend in the main cabin below decks on some large ship, and have with you some flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another, the distances being equal; jumping with your feet together, you pass equal spaces in every direction. When you have observed all these things carefully (though there is no doubt that when the ship is standing still everything must happen in this way), have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still. In jumping, you will pass on the floor the same spaces as before, nor will you make larger jumps toward the stern than toward the prow even though the ship is moving quite rapidly, despite the fact that during the time that you are in the air the floor under you will be going in a direction opposite to your jump…
In other words, the laws of physics work the same regardless of your (constant) rate of motion. There is no physical way to detect the presence, or absence, of absolute motion. The only thing that matters is relative motion between objects. This is relativity, in a nutshell: there is no such thing as absolute motion, only relative motion matters. On Earth, we call ourselves moving if we can see ourselves moving relative to the ground, or can feel ourselves moving relative to the wind; if you take away these considerations, as Galileo did by imagining himself in the cargo hold of a ship, there is no physical way to tell that you’re moving.
Of course, Galileo’s arguments (and his book) in favor of a Copernican solar system got him in trouble with the Catholic Church, and in 1633 (a year after the book’s publication) he stood trial for heresy in front of the Inquisition. He was forced to recant his theories, and his book was banned. This ban lasted until 1741, when a slightly censored version of the text was allowed to be published. (Oddly, as I’ve chronicled previously, there are still Biblical champions of the geocentric theory.)
The next step in developing the theory of relativity came from Isaac Newton (1643-1727), pictured below.

Newton made numerous contributions to the sciences, including important studies in optics, gravitation, and the development of calculus. He also made fundamental contributions to the study of mechanics (the study of how objects move when subjected to forces) which were compiled into his Mathematical Principles of Natural Philosophy (Philosophiae Naturalis Principia Mathematica). Here, Newton compiled his now famous three laws of motion, taken (in translated form) from his own words:
- The law of inertia: “Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.”
- The law of acceleration: “The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.” (F = ma)
- The law of reciprocal actions: “To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.”
We will not for now spend time discussing these laws. Newton, however, was aware of the works of Galileo and Copernicus before him, and it is to be noted that relativity is implicitly built into them. Before stating his laws, Newton spends quite some time discussing notions of “absolute” and “relative” space and time. To quote him again,
Hitherto I have laid down the definitions of such words as are less known, and explained the sense in which I would have them to be understood in the following discourse. I do not define time, space, place and motion, as being well known to all. Only I must observe that the vulgar conceive those quantities under no other notions but from the relation they bear to sensible objects. And thence arise certain prejudices, for the removing of which, it will be convenient to distinguish them into absolute and relative, true and apparent, mathematical and common.
…
IV. Absolute motion is the translation of a body from one absolute place into another; and relative motion, the translation from one relative place to another. Thus in a ship under sail, the relative place of a body is that part of a ship which the body possesses; or that part of its cavity which the body fills, and which therefore moves together with the ship: and relative rest is the continuance of the body in the same part of the ship, or of its cavity. But real, absolute rest, is the continuance of the body in the same part of that immovable space, in which the ship itself, its cavity, and all that it contains, is moved. Wherefore, if the earth is really at rest, the body, which relatively rests in the ship, will really and absolutely move with the same velocity which the ship has on the earth. But if the earth also moves, the true and absolute motion of the body will arise, partly from the true motion of the earth, in immovable space; partly from the relative motion of the ship on the earth; and if the body moves also relatively in the ship; its true motion will arise, partly from the true motion of the earth, in immovable space, and partly from the relative motions as well of the ship on the earth, as of the body in the ship; and from these relative motions will arise the relative motion of the body on the earth.
…
But because the parts of space cannot be seen, or distinguished from one another by our senses, therefore in their stead we use sensible measures of them. For from the positions and distances of things from any body considered as immovable, we define all places; said then with respect to such places, we estimate all motions, considering bodies as transferred from some of those places into others. And so, instead of absolute places and motions, we use relative ones…For it may be that there is no body really at rest, to which the places and motions of others may be referred.
There’s a lot to digest in those excerpts, but we can summarize them relatively concisely.
The first excerpt observes that understandings of space, time and motion that arise from everyday experience lead one to certain ‘prejudices’, or misunderstandings, about the nature of these quantities. In particular, there is a confusion concerning the ideas of ‘absolute’ and ‘relative’ motion. These seem to be the same misconceptions we discussed earlier in the context of Galileo’s work.
The second excerpt first discusses ‘relative’ and ‘absolute’ motion. Using what is likely a Galileo-inspired example of an object in a ship’s hold, Newton points out that the ‘absolute’ motion of an object inside a moving ship is quite complicated: one must account for the motion of the object within the ship, the motion of the ship on the Earth, and the motion of the Earth with respect to some ‘absolute’ reference point.
In the third excerpt Newton observes that, even though there may be an ‘absolute’ reference point in space from which all motion should be measured, we do not know where that point is and must therefore work only with relative motions of objects.
This ‘Newtonian principle of relativity’ is the observation that Newton’s laws work just as well for any observer moving with constant velocity. To put it in more physical terms, all observers agree on the forces involved in some sort of motion. If two cars collide on the road, measurements of the force of impact by an observer standing by the side of the road and by an observer driving by on the opposite side of the road will be in agreement.
Newton’s observation that the laws of physics work equally well for all observers moving at constant speed held for two centuries. In Newton’s time, however, the only clearly established laws of physics were Newton’s formulas which described how forces related to motion. By the late 1800s, a new set of formulas had been established, by James Clerk Maxwell (1831-1879), pictured below.

Before Maxwell’s time, it was known that electric and magnetic forces were related to one another, but a complete description of their relationship was lacking. In 1864, this scruffy-bearded scientist presented a set of equations to the Royal Society which gave a complete description of electromagnetic phenomena. Furthermore, Maxwell demonstrated that his equations predicted the existence of electromagnetic waves, and further suggested that light is an electromagnetic phenomena, a suggestion which is now well-known to be true. In Maxwell’s own words,
The agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws.
For completeness, we present Maxwell’s equations in free space, in modern mathematical parlance, below:
,
,
,
.
(There are, of course, multiple forms of Maxwell’s equations, depending on the system of units chosen. I’m using the theorist-friendly Gaussian system.)
A problem arises when applying Newton’s version of relativity to Maxwell’s equations: two people observing the same electromagnetic phenomena with different speeds will evidently have different opinions on the forces involved! We can illustrate this with a simple thought experiment: suppose we have a single electric charge q situated a distance d from an electrically charged wire with charge density (charge/meter) λ:
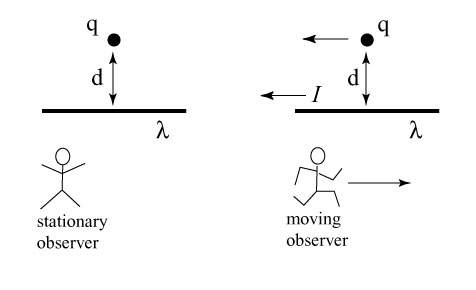
The observer on the left will see an electric force of magnitude repelling the point charge and the wire. Under Newtonian relativity, the moving observer on the right will see the same electric force. However, for the moving observer, the point charge and the line charge appear to be moving. The line charge will therefore also appear to be carrying a current I. This means there should also be a magnetic force between the line and the point also repelling them. The combination of Newtonian relativity and Maxwell’s equations suggests that the moving observer and the stationary observer come to different conclusions about the amount of force exerted between the wire and the point charge! This is a very unusual conclusion; returning to our earlier example of a car accident, it is comparable to saying that a stationary witness to the accident sees both cars totaled while the moving witness claims it was only a fender-bender!
Both observers cannot be right. Physicists at the time were faced with a choice: either Newtonian relativity, and implicitly Newton’s laws, were incorrect or incomplete, or relativity simply didn’t hold for Maxwell’s equations. This latter option brings back the idea that there is a ‘special’ frame of motion in which Maxwell’s equations are true: an observer moving in that frame of motion has the ‘correct’ view of electromagnetic waves, and everyone else is ‘wrong’.
This didn’t seem quite so outlandish at the time. Once it had been determined that light was an electromagnetic wave, it was natural to ask what medium carried that wave. After all, water waves are carried in water, and sound waves are carried in air. By analogy, one would expect that there exists some previously undiscovered medium whose vibrations created light waves. This medium was dubbed ‘the aether‘, and it was assumed that the ‘correct’ frame of reference was an observer standing still with respect to the aether.
The next logical step, if the aether existed, would be to measure its properties somehow. If the Earth moves through the aether, the speed of light as measured on Earth should depend on how fast it moves relative to the aether. Experimentalists began to try to measure this motion, and their inability to detect any ‘aether drift’ led to Einstein’s scientific revolution.
In the next post, we’ll discuss experimental techniques to measure the speed of light, including the famous Michelson-Morley experiment. Once we have seen the outcome of their experiment, we’ll be well positioned to understand why Einstein needed to develop a new theory of relativity.


I wish you had been my physics teacher in college. 🙂
Thanks Janet!
From this article I have learned that brilliant physicists have a lot of hair on their heads, either on their chins (Galileo and Maxwell) or on their scalps (Newton and Einstein). You are just a skull with no hair whatsoever. How can we possibly trust your mad ravings?
PD wrote: “You are just a skull with no hair whatsoever. How can we possibly trust your mad ravings?”
You’re assuming that brilliant physicists have to have hair on their head…
SkullsInTheStars wrote: “You’re assuming that brilliant physicists have to have hair on their head…”
[shudder, shudder, shudder]
Question fearfully withdrawn.
PD: Where did you think I was referring to? You’ve got a sick mind…
Where exactly were you referring????
babs67: Now I’m not telling! 😛
I have seen in your text, for the first time in a clear and straight-forward manner, an explanation of why many think that Maxwell laws threatened the principle of relativity. However, I still do not see the point. A man standing on a train drops a ball on the floor, which is at rest with the ball in as much as lateral motion is concerned. I head with my car towards the train and see both the floor of the train and the ball approaching me. Well, that means that, for the purpose of my survival, I had better change direction to avoid a crash, because the floor of the train is a “current” moving towards me. But if I calculate the forces between the ball and train, then I compare the motion of the ball RELATIVE TO the train and so I do not imagine that, for this purpose, there is any “current” under the ball. Could you please correct me if I am wrong?
Pingback: Relativity: Measuring the speed of light | Skulls in the Stars