In previous posts, I’ve talked at some length about computed tomography (CT) and optical coherence tomography (OCT). Each of these is a technique for determining information about the internal structure of an object, such as the human body, from exterior measurements of the scattering of electromagnetic waves from the object. In the case of CT, x-rays are used to measure and image a cross-sectional ‘slice’ of the human body, while in OCT, broadband visible light is used to probe a few millimeters into the skin or an internal organ of the human body.
Plenty of other techniques exist for measuring the internal structure of objects, using a variety of different types of waves. Magnetic resonance imaging (MRI) subjects a patient to an intense magnetic field, and makes an image by measuring the radio waves emitted when the field is suddenly switched. Ultrasound imaging uses ultrasonic waves to probe the soft tissues of the human body, and is used in mammography.
Each of these techniques is quite different in its range of application, but all require nontrivial mathematical techniques to reconstruct an image from the raw scattered wave data. These mathematical techniques are broadly grouped into a class of problems known as inverse problems, and I thought it would be worth an optics basics post to discuss inverse problems, their common features, and the challenges in solving them.
So what is an inverse problem? In the most general sense, we may consider an inverse problem to be the determination of the “cause” of a phenomenon from measurements of the “effect” (i.e. the phenomenon itself). Every inverse problem is based upon a corresponding forward problem whose solution represents the usual “cause-effect” sequence of events. In other words:
- Forward problem: Given the “cause”, determine the “effect”
- Inverse problem: Given the “effect”, determine the “cause”
Traditional physics problems are typically “forward problems”, though not usually described as such. Examples include:
- Given two particles colliding together at high speed and the forces of interaction (cause), determine their behavior at a later time (effect)
- Given a scattering object and a light field shining upon it (cause), determine the behavior of the scattered field (effect)
- Given a collection of oscillating electric charges and currents (cause), determine the electromagnetic field radiated by the collection (effect)
Each of these forward problems has a relevant inverse problem associated with it:
- Given the behavior of particles (effect) which have undergone a collision, determine the forces of interaction (cause)
- Given the field scattered by an object (effect), determine the internal structure of the scattering object (cause)
- Given the radiation field of a collection of charges/currents (effect), determine the structure of the collection (cause)
Each of these problems is of great practical importance. The first one, deducing the forces of interaction based on the scattering of particles, is essentially the task of high-energy physicists. The second one, determining the structure of an object from the scattered field, is referred to as an inverse scattering problem and includes the techniques of CT, OCT, and MRI. The third one, determining the structure of a collection of electromagnetic sources from the radiation pattern, is known as an inverse source problem and is important in the design of antennas.
We will see that the idea of an inverse problem has some merit even outside the realm of science. As a morbid example, a crime scene investigation is a sort of inverse problem. The investigator’s goal is to determine the “cause” of the crime (the criminal and his motive) from measurements of the “effect” (evidence left behind at the crime scene). This example will work quite well in discussing some of the difficulties in solving inverse problems.
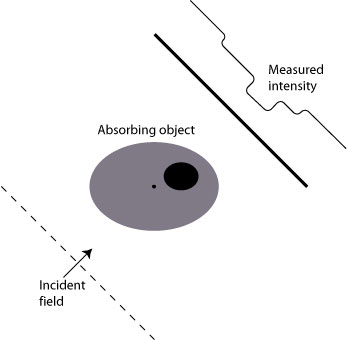
Heck, even vision is in essence a sort of inverse problem: we use our eyes to receive light scattered from distant objects (effect) and thus deduce the shape/distance/color of the object (cause). Modern inverse problems in physics, however, involve complicated data collection schemes which only produce a recognizable image after significant mathematical processing of the data. In computed tomography, for instance, an image is made up of a large collection of individual ‘shadowgrams’; an illustration of one such shadowgram is shown below:
The ‘image’ measured at the detector is a measure of the cumulative absorption of x-rays on passing straight through the body; this is not enough information to map the complete internal structure of the patient. To get this structure, one must make multiple measurements, for a variety of directions of illumination, and combine these measurements in an appropriate way via computer:
The first step in solving an inverse scattering problem, then, is determining how an individual measurement of the scattered field relates to the overall structure of the scatterer.
This is where theorists like myself have lots of fun with inverse problems: starting with the physics equations that describe the forward problem, we try and turn them ‘inside out’ to get a formula for the inverse problem.
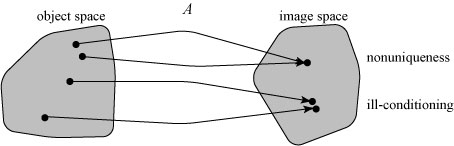
Many inverse problems, however, are said to be ill-posed, in a sense first described by the mathematician Jacques Hadamard in 1902. A problem which is ill-posed suffers from at least one of two problems: nonuniqueness in the solution of the problem and large errors in the solution which follow from small errors in the data. The first problem is simply referred to as nonuniqueness and the second is referred to as ill-conditioning.
This is where our example of a crime scene investigation is illustrative! It is certainly possible that there may not be enough evidence at the scene to identify a suspect, or the evidence may point equally to multiple suspects! In such a case the solution of the crime, based on the evidence at the scene, is nonunique. It is also possible that a piece of evidence may lead investigators to the wrong suspect entirely; in such a case, the solution is ill-conditioned. (In the movie Presumed Innocent, for instance, Harrison Ford’s character is put on trial for murder based on his fingerprints being present on a glass at the crime scene. It is later revealed that the glass was present at the scene for a quite unexpected reason.)
We can illustrate these problems with a diagram. Suppose we have a collection of ‘objects’ (causes) which are turned into ‘images’ (effects) by the action of an event A. A good inverse problem will ideally have a unique mapping of one image for each object. If two objects result in the same image, we have nonuniqueness. Even if there is a unique correspondence between each object and image, two very different objects may produce very similar images. In this case we have ill-conditioning. These are illustrated below:
Can we overcome obstacles such as nonuniqueness and ill-conditioning? Sometimes! The most common, general type of resolution is the use of so-called prior knowledge. It is often the case that we have additional information about the ‘object’ beyond the measurements made in the experiment. We can use this information to rule out solutions which conflict with this additional knowledge. With the right amount of prior knowledge, we can (hopefully) make the solution of the problem unique and stable. This is diagrammed below:
A good example of applying prior knowledge is in the so-called phase problem in optics. Coherent wavefields are described at each point in space by their amplitude (brightness) and their phase (roughly, direction of travel). Detectors typically only measure the amplitude (intensity) of the wavefield, although the phase often contains equally if not more important information. But the phase and amplitude of a wavefield are related to one another, and a natural question arises: can one deduce the phase from intensity measurements alone? In principle, the problem is nonunique: many different phase structures can be associated with a single intensity pattern. However, most of these phase structures are unphysical, in that they could only be produced by an extremely large or infinite source. With the prior knowledge of roughly the size of the source, one can eliminate most of the incorrect solutions.
In our example of a crime scene, prior knowledge would be any additional information acquired outside the scene itself. A cigar at the crime scene would not in itself point to a single person, but if we know from other investigations that only 5 people could have visited the crime scene that night, and only one of them is a smoker, we have more definitive evidence.
For problems which are ill-conditioned, another technique has been developed to provide a stable solution, known as regularization. It is a way to ignore or throw out those parts of the inversion process which are particularly sensitive to noise in the data.
It is interesting to note that there is a connection between the nonuniqueness of an inverse problem and the existence of ‘invisible’ objects in that problem, a topic I’ve discussed before. The inverse source problem, mentioned above, is a good example of this relationship: Suppose we have a collection of oscillating charges/currents; can we determine the form of this collection from measurements of the radiation emitted by the collection?
It turns out that you can’t! There exist sources, now generally referred to as nonradiating sources, which (theoretically, at least) produce no electromagnetic radiation outside the region of the charges/currents. The existence of such sources makes the inverse source problem nonunique: one cannot be sure, using radiation measurements alone, that an arbitrary source does not possess a component which is nonradiating.
We find somewhat the opposite effect in the case of the inverse scattering problem: the non-existence of nonscattering scatterers suggests that there is a unique solution to the inverse scattering problem. It has been shown that no scatterer exists which is nonscattering for all directions of illumination (with an interesting caveat, to follow). In other words, one may theoretically construct an object which looks invisible for a finite number of directions of illumination, but not one that is invisible to all directions. This actually can be connected to a practical consequence: in CT, errors in the image (artifacts) can arise if insufficient data is taken.
The interesting caveat to this is that, as we’ve discussed before, researchers have demonstrated that one can make an (in principle) perfect invisibility device by using optically anisotropic materials. This suggests that the inverse scattering problem for anisotropic materials is nonunique, which in turn suggests all sorts of weird things (which I’m currently looking into, so I’ll say no more… for now!).
It is worth noting that the solution of inverse problems can be used not only for the analysis of objects (such as the analysis of the human body performed by CT and OCT), but also for synthesis: the construction of objects with specified properties. For example, in the construction of antennas, it is of interest to design them with specific radiation properties. Knowing the type of field desired, one can use the inversion algorithms to determine the appropriate antenna structure. In this case, nonuniqueness is a good thing: more solutions means more versatility in designing the antenna!
Even with the abundance of medical imaging techniques, the study of inverse problems remains important. Part of the reason for this is the reality that every technique in existence has some sort of limitation; for instance:
- Computed tomography: uses x-rays, which are ionizing radiation
- Magnetic resonance imaging: non-ionizing radiation, but device is prohibitively expensive
- Optical coherence tomography: uses visible light, but has small penetration depth into tissue
- Ultrasound: Excellent for probing soft tissues, but low resolution can potentially miss tumors
Each new technique is tailored to its own specific application, and new techniques are proposed all the time. It will be interesting to see what the next generation of imaging devices looks like!




Don’t forget another type of inverse problem important to astronomers – gravitational lensing. You call get all sorts of interesting information about galaxies and cosmology using lensing that we have no other way to access.
meichenl: Thanks for the comment! There are plenty of inverse problems that would each merit their own post. Applying gravitational lensing to imaging is certainly an interesting one.
Thanks for another illuminating post! (pun intended 🙂
It’ll probably take me the rest of today to finish learning about all the interesting things you mentioned. My own research concerns only the forward problem, so it’s very instructive for me to consider this totally different point of view.
Wade: I’m glad it made sense!
dear sir,
Iam a phd student in indian institute of science. my research area is inverse problems, specifically optical and elastic property reconstruction of breast tissue using diffuse correlation tomography. I found this article on inverse problem easily understantable, well presented, and thought provoking. I have also gone through the article on cloaking devices. Let me thank you for posting such articles which can even be read and understand by an amateur.
yours sincerely
hari .
hari: Thanks!