Infinite series are weird — redux!

A bit over a year ago, I wrote a blog post about the mathematics of infinite series, and how weird such series can be, considering in particular the behavior of “conditionally convergent series”. A recent post at Built on Facts covered similar oddities and gave a nice and different perspective on them. In the comments of that post, though, an even more bizarre result from the theory of infinite series was introduced, namely the argument that

$\displaystyle 1+2+3+4+\ldots = -1/12$ .

This result, if true, is enough to shake one’s faith in mathematics, and is completely non-intuitive for no less than three very big reasons:

The sum of an infinite series of increasing positive integers should not converge to a negative value,
The sum of an infinite series of increasing positive integers should not converge to a fractional value,
The sum of an infinite series of increasing positive integers should not converge at all to a finite value!

So is the equation above correct? Not exactly; it is based on a valid bit of mathematics centered on the Riemann zeta function, but that mathematics is being somewhat misinterpreted to get the paradoxical equation. An explanation of what went wrong is interesting in itself, however, and allows me to describe a rather difficult concept in the theory of complex analysis known as analytic continuation.

Before we address the weird infinite series shown above, we first consider the behavior of more familiar series, the geometric series, defined as

$\displaystyle S = 1+ x+x^2+x^3+\ldots = \sum_{n=0}^\infty x^n$ .

(See my previous blog post for an explanation of the notation.)

It can be seen relatively easily that this series has an infinite or undefined sum for values of $|x|\geq 1$ . For $x>1$ , each term is larger than the previous one, and the sum just becomes larger and larger as more terms are added. For $x<-1$ , the magnitude of each term is larger than the previous one, so the sum “swings” between increasingly larger positive and negative values as more terms are added. For $|x|=1$ , similar arguments apply.

It is not necessarily clear, however, that the series has a sum for $|x|<1$ ; we can prove that this is the case, however, and find an explicit, simple expression for this sum as follows. We introduce a sequence of partial sums $S_N$ of the form

$\displaystyle S_N = 1+x+x^2+\ldots+x^N = \sum_{n=0}^N x^n$ .

This expression represents the sum over the first $N$ elements of the infinite series. In the limit $N\rightarrow\infty$ , we recover the infinite series itself.

To determine an explicit expression for the sum of the infinite series, we note that the sequence of partial sums satisfies two identities:

$\displaystyle x S_N = x+x^2+\ldots+x^{N+1} = S_{N+1}-1$ ,

$\displaystyle S_N = 1+x+x^2+\ldots+x^N = S_{N+1}-x^{N+1}$ .

If we take the difference of these two equations, we end up with the relationship:

$\displaystyle (1-x)S_N = 1-x^{N+1}$ ,

which may be solved for $S_N$ of the form:

$\displaystyle S_N = \frac{1-x^{N+1}}{1-x}$ .

We determine the sum of the infinite series by considering the limit as $N\rightarrow \infty$ . Provided $|x|<1$ , we can see that the term $x^{N+1}\rightarrow 0$ and the sum of the infinite series reduces to the form:

$\displaystyle S= \sum_{n=0}^\infty x^n = \frac{1}{1-x}$ .

For $|x|<1$ , the sum of the infinite series therefore has the simple mathematical form $1/(1-x)$ . This latter function, however, is well-defined for all values of $x$ except the value $x=1$ .

From a philosophical point of view, we may consider the infinite series $S$ to be a representation of the “true” function $T=1/(1-x)$ ; the representation is only valid when $|x|<1$ .

This is a simple example of what is referred to as analytic continuation. When dealing with a class of sufficiently well-behaved functions (known as analytic functions), one often finds a representation of the function that is valid over only a limited domain. It is possible, however, to mathematically find the value of the “true” function everywhere through the process of continuation. The geometric series is a simple example of this process: we began with the series $S$ which is valid only for $|x|<1$ , but were able to show that this is a representation of the function $T$ which is valid for all $x\neq 1$ .

This argument applies to the geometric series with complex argument, as well; that is, if we replace $x$ by $z=x+iy$ , with $i = \sqrt{-1}$ , we find that

$\displaystyle S= \sum_{n=0}^\infty z^n = \frac{1}{1-z}$ ,

which converges for $|z|<1$ , while the function $T=1/(1-z)$ is well defined for any $z\neq 1$ .

For our purposes, we state this result in a slightly different way: the function $T=1/(1-z)$ is valid for all $z\neq 1$ , but it only represents the infinite series $S$ for $z$ -values such that $|z|<1$ .

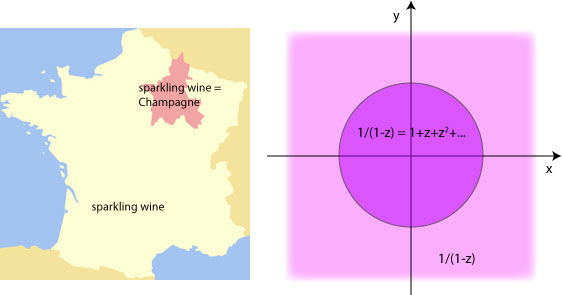
The best analogy I can make to this is to consider sparkling wine production in France: sparkling wine is produced in every province of France, but only in the province of Champagne is that sparkling wine also called “Champagne”:

If this seems confusing to you, you’re not alone: concepts related to analytic continuation are some of the most difficult to grasp in studying analytic functions.

How does this relate back to the summation $1+2+3+4+\ldots = -1/12$ ? Let us now introduce a series known as the Dirichlet series, defined as

$\displaystyle D(z) = 1+\frac{1}{2^z}+\frac{1}{3^z}+\frac{1}{4^z}+\ldots = \sum_{n=1}^\infty \frac{1}{n^z}$ .

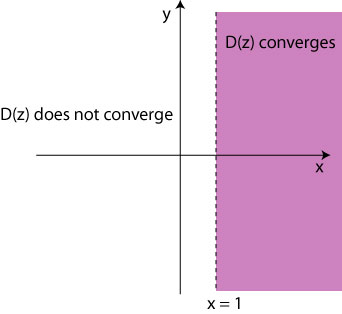
It can be readily shown that this series will converge for all values of $z=x+iy$ such that $x>1$ :

This means that the series does not converge for the choice $z=-1$ , which represents the series:

$\displaystyle D(-1) = 1 +2 + 3+ 4+5 +\ldots$ .

However, the Dirichlet series can be analytically continued to a function that is well-behaved for all values of $z$ , except $z=1$ ; this function is known as the zeta function, $\zeta(z)$ . For $z=-1$ , the zeta function can be shown to take the value :

$\displaystyle \zeta(-1)=-\frac{1}{12}$ .

This is the explanation of the bizarre result introduced at the beginning of this post. The Dirichlet series itself does not converge to any sensible value at $z=-1$ , but its analytic continuation, the zeta function, is defined at that point. From a strictly mathematical point of view, the equation $1+2+3+4+\ldots = -1/12$ is incorrect, and involves confusing the Dirichlet series with the zeta function.

The zeta function is an interesting beast in itself. It is intimately related to the prime numbers, and it can be shown that it may be written in the form

$\displaystyle \prod_{p \mbox{ prime}}^\infty \frac{1}{1-p^{s}}$ .

The symbol $\prod$ indicates an infinite product, and $p$ ranges over all the prime numbers. Entire books have been written on the mathematical properties of the zeta function.

One of the great unsolved problems of mathematics is related to the distribution of the zeros of the zeta function; it is known as the Riemann hypothesis, and its resolution would have a huge impact on number theory and our understanding of prime numbers.

So we have seen that in mathematics, the series $\displaystyle 1+2+3+4+\ldots$ does in fact diverge, and one would expect that such a series would not have any sensible physical meaning. But here’s where things get weird: in the study of the quantum theory of electromagnetism, one encounters series such as $D(-1)$ . Superficially, one would expect that the derivation must be incorrect, but results quantitatively consistent with experiment can be derived if one replaces $D(-1)$ with $\zeta(-1)$ !

An example of this involves the Casimir effect, first introduced in 1948. In short, it is known that empty space, i.e. vacuum, is never truly empty, but includes “virtual photons” that wink in and out of existence. These virtual photons can be influenced by metal boundaries, just like real photons, and when two metal plates are placed close together, the virtual photons are “squeezed” out of the region between them. The imbalance in virtual photons outside and inside the plates produces a net inward pressure, which can be detected by experiment (source):

The calculation of the Casimir force is outside the scope of this post, but it requires an infinite summation over all the allowed energy states between the plates, of the form

$\displaystyle \sum_{n=1}^\infty n^3$ .

This sum is simply the Dirichlet series $D(-3)$ ; if we naively interpret this sum as a zeta function, we get the result

$\displaystyle \sum_{n=1}^\infty n^3 = \zeta(-3)= -1/120$ .

If this result is used in the Casimir calculation, the result is quantitatively correct!

It’s hard to know what exactly to make of this. It is to be noted that, mathematically, it is unambiguously true that the series $D(-1)$ diverges; however, it seems that in quantum field theory the analytic continuation of this series gives the proper result.* There seems to be something very deep in that statement, but I’ll be darned if I know exactly what it means.

In any case, this post shows again that infinite series can be very weird!

********************************

* It is also worth noting that Casimir used a different approach to determine the sum in his original paper, and didn’t use the zeta function explicitly.

14 Responses to Infinite series are weird — redux!

Blake Stacey says:

May 25, 2010 at 5:32 pm

The physical intuition is that if you actually do the experiment to measure the Casimir force, you’re using metal plates which are not ideal conductors. It takes time for electrons to move through them to set up electric fields to cancel incident fields. Photons of sufficiently high frequency can slip through; they won’t be confined between the plates. So, we have to incorporate a high-frequency cutoff into the sum over all allowed energy states.

You can find the details in David Tong’s quantum field theory notes (p. 27 in chapter 2).

- skullsinthestars says:
  
  May 25, 2010 at 8:40 pm
  
  Thanks for the comments, and links! I was more or less aware of the physical interpretation to regularize the Casimir equations: Casimir himself essentially used that argument in his paper (I was thinking of coming back to discuss the physics of the Casimir force at a later date). I hadn’t seen the regularization techniques that mathematicians were using for the zeta.
  
Blake Stacey says:

May 25, 2010 at 5:36 pm

Terry Tao (Fields medalist, general mathematics guru) had a nice blog post on “zeta function regularization” a while back, showing what happens when the mathematicians take physical intuition about high-frequency cutoffs and make it all spiffy.

zerology says:

May 27, 2010 at 5:59 am

As T. Pratchett said: “Nobody knows the meaning of all this, but its probably quantum.” (Pyramids, Pyramids)

Donald S. McDonald says:

April 4, 2011 at 5:40 pm

oeis A070891. Denominator of Sum_{k=1..n} mu(k)/k when it changes sign IS SQUARE FREE ?? up to primorial 43. Partial harmonic series with mobius function coefficients. Wellington, New Zealand. WHY !!

Chris Locke says:

October 12, 2011 at 6:00 am

Blake is right when he says that one can use a cutoff regulator to get the same result as just simply substituting in the value of D(-3). Another similar thing happens in field theory involving the geometric series. When we calculate the exact propagator (accounting for self-interactions), we end up with a geometric series with “a” equal to the interaction-less propagator, and the “r” being a typically divergent quantity (for reference, it is the sum of 1 particle irreducible diagrams). Even though this total sum is highly divergent in our case, we realize that we got this value using perturbation theory, so we just make the assumption that this series can be replaced by its analytical continuation a / (1 – r).

rknop says:

January 17, 2014 at 11:25 am

Isn’t subtracting infinity from infinity and interpreting the remainder as physically meaningful the very basis of quantum field theory?

Pingback: An infinite series of blog posts which sums to -1/12 | The Aperiodical
Pingback: Halloween Manifestos, 2013 « Log24
lenx says:

March 17, 2015 at 9:31 am

Hi Guys.

I really enjoyed this post and wanted to suggest to all interested parties on these Numberphile the videos with the subject:

ASTOUNDING: 1 + 2 + 3 + 4 + 5 + … = -1/12 – https://www.youtube.com/watch?v=w-I6XTVZXww

Sum of Natural Numbers (second proof and extra footage) – https://www.youtube.com/watch?v=E-d9mgo8FGk

One minus one plus one minus one – Numberphile – https://www.youtube.com/watch?v=PCu_BNNI5x4

Anyway, hope you enjoy … !!!!!!!!!!!!!!

Bye Now …

Pingback: The Sum Of All Numbers Is -1/12? – This Week I Found Out
Pingback: Infinite series are weird — redux! | Blog.CarlRobitaille.org
Ángel Méndez Rivera says:

December 10, 2018 at 3:35 am

This post spreads too much misinformation.

In the Casimir force, the particles involved are not virtual photons of any sort because they cannot be said to even have the properties of photons at all. You obviously fail to understand what makes a particle of a certain type precisely a particle of that type.

- skullsinthestars says:
  
  December 10, 2018 at 10:07 am
  
  Dude I teach math and theoretical physics. As a full professor. Take your arrogant attitude elsewhere. And learn the difference between a rigorous scientific paper and a popular science blog post.