(This is a continuation of my “history of invisibility physics” series of posts. The earlier posts are: Part I, Part II, Part III, Part IV, Part V, Part VI)
The history of invisibility physics truly began with the concept of radiationless motions of charged particles, as described by Ehrenfest in 1910 and Schott in 1933. There are many more discoveries associated with these and related phenomena, which would eventually be referred to as nonradiating sources.
I would like to jump ahead in the history a little bit, however, and discuss a paper published in the Journal of the Optical Society of America in 1975 by Milton Kerker, entitled, “Invisible bodies”. The article, relatively unknown today, is the first article to describe an object which is invisible in the true sense of the word — although the object itself is microscopic!
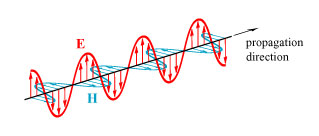
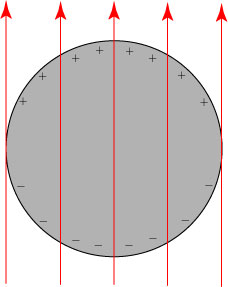
To understand how Kerker’s invisibility theory works, we need first to understand how light interacts with matter and is scattered by it. We start by recalling that light is a transverse electromagnetic wave, with electric field E and magnetic field H that oscillate perpendicular to each other and transverse to the direction of motion:
(For those not familiar with depictions of electromagnetic fields: the arrows are an indication of the strength and direction of the electric (red) and magnetic (blue) fields along the line. A positively-charged particle will experience a force in the direction of the red arrow.)
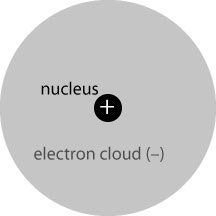
So what happens when such an electromagnetic wave hits matter? We begin by considering the simplest useful case: a static uniform electric field* interacting with a single hydrogen atom. The hydrogen atom is, in essence, a very small and heavy positively-charged nucleus, and a quantum-mechanical electron “cloud” of equal and opposite charge to the nucleus. We may picture it as follows:
The atom is overall electrically neutral; because the nucleus and cloud are concentric, their electric fields are of the same form and cancel completely outside of the electron cloud.
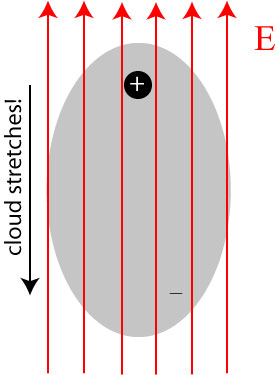
When an electric field is applied to an atom, positive charges are pulled in the direction of the field, while negative charges are pulled in the direction opposite of the field (this is, in essence, derived from Coulomb’s law). In bulk matter, the nuclei are typically too heavy and locked into place to move when the field is applied, but the electron cloud is twisted and stretched away from the nucleus:
The result is that the atom, though its overall charge is negative, produces its own electric field, because the positive and negative charges are spatially separated! In fact, the cloud may, to a reasonable approximation, be treated as being localized around its center, and the positive and negative charges together form what is known as an electric dipole:
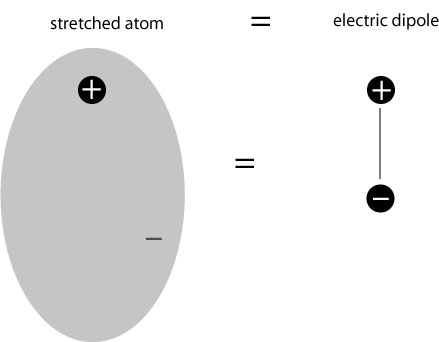
The term “dipole” = “two poles”, referring to the fact that the charge distribution consists effectively of two distinct separated charges of opposite sign. The electric field produced by the dipole is itself quite complicated, but it points from the positive charge to the negative one; an illustration showing the flow of the field is given below:
(The arrows in this case indicate the direction of the force a positively-charged particle would experience if placed in that region of space.)
So when an electric field is applied to a neutral atom, it separates the charges of the atom into a dipole, which produces its own, secondary, electric field. It is to be noted that the electric field produced by the atom is in the opposite direction of the applied field, and therefore tends to cancel it.
We now imagine a light wave illuminating a single atom. A light wave is an oscillating electromagnetic wave, and part of the energy of that wave sets the electron cloud oscillating, converting the atom into an oscillating dipole. This oscillating dipole produces its own oscillating electromagnetic light wave, which radiates in all directions. This, in short, is the process by which a light wave is scattered by an atom.
In optics we are most often interested in the scattering of light from bulk material, which is a large collection of atoms all stuck together. We now take a few paragraphs to see how the arguments above change when an electric field interacts with a bunch of atoms at once.
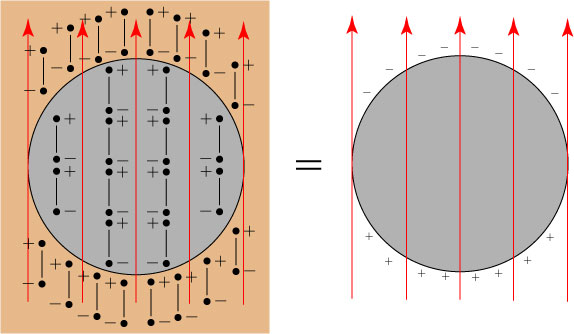
Let us imagine a uniform spherical object subjected to a static electric field. The sphere is, of course, made of many atoms, but we will depict it by a small number of them. Each atom gets turned into a dipole by the applied electric field**, and we have a situation as follows:
It should be noted that, in the interior of the sphere, the “+” and “-” charges of different dipoles get squeezed together: these interior charges effectively cancel out, and the only place where a net charge remains is on the boundary of the sphere:
We end up with positive charges on the top of the sphere, and negative charges on the bottom of the sphere: in essence, the entire sphere ends up looking like one big dipole!
Let us now consider a case where the sphere is surrounded by a material that has a larger density of dipoles (or, equivalently, stronger dipoles). In physics, this is characterized for a given material by a quantity called the permittivity, and typically labeled . The permittivity is a measure of how readily electric dipoles are induced in matter when an electric field is applied.
Because the outer material is assumed to have a larger permittivity than the sphere, it will have a larger imbalance of charge on the boundary than the inner material; the sphere will end up looking like a dipole with negative charge on top:
The embedded sphere acts like a dipole that is the opposite of the dipole of the sphere in air: the air sphere has positive charge on top, the embedded sphere has positive charge on the bottom. The two spheres will also produce electric fields that are opposite one another, and if an electromagnetic field is scattered from the two different types of sphere, the electromagnetic waves produced will be opposite of one another.
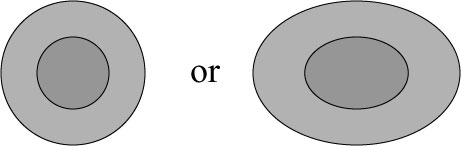
This is the observation that forms the basis of Kerker’s theory of invisible bodies***. Kerker considered scattering objects that are concentric spheres or, more generally, confocal ellipsoids, of the form:
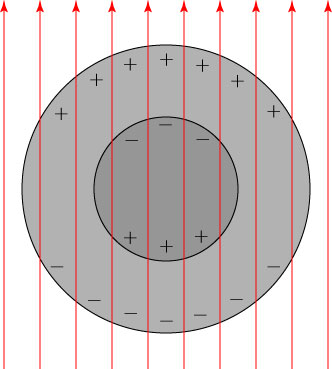
Let us suppose that we have such a sphere, with a larger permittivity in the outer layer than the inner layer. Then the outer surface and the inner surface get charges induced on them, and the outer shell and the inner sphere each act like dipoles, but of opposing direction:
The electric fields produced by the “inner sphere dipole” and the “outer shell dipole” therefore tend to cancel each other out; Kerker showed that if the radii of the spheres and their permittivities are chosen properly, one can get the electric fields of these two dipoles to cancel exactly. If we illuminate this Kerker sphere by an electromagnetic wave, the scattered waves produced by the inner dipole and the outer dipole will cancel each other out exactly, and there will be no scattered field. An illuminating light field will pass right through the object without being scattered, and the object will be invisible!
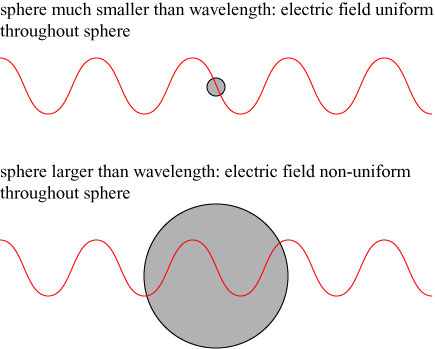
There is one caveat to the argument that we have made above: it applies only to an object illuminated by a uniform electric field, while an electromagnetic wave is a non-uniform, oscillating wave. However, if our spherical object is much smaller than the wavelength of light in size, then at any time the electric field passing through it is approximately uniform, and the above discussion is appropriate:
Kerker’s form of invisibility only applies, therefore, for spheres that are less than the wavelength of light, which is roughly meters; Kerker’s invisible bodies are necessarily microscopic.
The simplifying approximation that the field is uniform over particles much smaller than the wavelength is, incidentally, referred to as Rayleigh scattering; Lord Rayleigh (1842-1919) introduced this approximation to demonstrate that the blue sky is caused by sunlight scattering off of the small particles, atoms, and molecules that constitute the atmosphere.
Milton Kerker himself is clearly a very clever fellow, and was in fact a leading researcher in his time into the study of light scattering by small particles; he published a book entitled “Scattering of Light & Other Electromagnetic Radiation” in 1969. We will see his name come up again at least once more in the history of invisibility physics.
Kerker’s microscopic “invisible bodies” are a far cry from the modern conception of an “invisibility cloak”, but they represent the first demonstration that it is possible to design an object that does not scatter light. It is a forgotten milestone in an intriguing and odd field of optical science.
My favorite part of Kerker’s paper, however, is his acknowledgment of financial support:
This research was supported in part by the Paint Research Institute in connection with a numerical study of the effect of microvoids upon the hiding power of paints.
Kerker’s optical research was sponsored by a paint company! I use this example to explain to students that they should be imaginative in seeking out new sources of funding — you never know who might have a use for your crazy ideas!
*************************************
* In optics, the magnetic field typically has little influence on the scattering of light, and can be safely neglected; in his paper, though, Kerker points out that his results can change drastically if the material properties of the object allow magnetic effects.
** The situation is actually much more complicated when more than one atom is present. The applied field makes the atoms into electric dipoles, which each produce their own electric fields. The dipoles then influence each other through their induced electric fields, which causes the dipoles to change, which causes their fields to change, which causes the dipoles to change, ad nauseum. To rigorously deal with the effect of an applied electric field on matter, the system of applied field and dipole fields much be solved in a self-consistent matter.
*** M. Kerker, “Invisible bodies,” J. Opt. Soc. Am. 65 (1975), 376-379.




Nice description of a complicated subject.
One that I will reread.
Thanks me man 🙂
Thanks! It certainly took a lot of effort to make it comprehensible!
Pingback: The Development of Data Projectors | Australian Mining Blog
Pingback: The Giant’s Shoulders #25: 2nd Anniversary Edition! « The Dispersal of Darwin
Pingback: Open Laboratory 2010 – submissions so far « A Blog Around The Clock
Pingback: Open Laboratory 2010 – submissions to date « A Blog Around The Clock
Pingback: Open Laboratory 2010 – submissions so far « A Blog Around The Clock
Pingback: Open Laboratory 2010 – submissions so far | A Blog Around The Clock
Pingback: Open Laboratory 2010 – three weeks to go! | A Blog Around The Clock
Pingback: Open Laboratory 2010 – three weeks to go! | A Blog Around The Clock
Pingback: Open Laboratory 2010 – two weeks to go! | A Blog Around The Clock
Pingback: Open Laboratory 2010 – only eight days till the deadline! | A Blog Around The Clock
Pingback: Only three days to go – Open Laboratory final stretch for submissions! | A Blog Around The Clock
Pingback: It’s getting hot – submissions for Open Laboratory 2011 are flying in by the dozens per hour… how about you? | A Blog Around The Clock
Pingback: Open Laboratory 2010 – the final stretch! | A Blog Around The Clock
Pingback: Open Laboratory 2010 – submissions now closed – see all the entries | A Blog Around The Clock
Pingback: Open Lab 2010 finalists « Seeds Aside