![]() I don’t often talk about my own research on this blog… heck, I don’t think I’ve ever talked about my own research here, come to think of it! I thought it would be a nice change of pace to describe a paper that recently appeared in the journal Plasmonics of which I am a co-author. The paper, titled, “Coherence converting plasmonic hole arrays”, describes how one can use an array of subwavelength-size holes in a thin metallic screen to alter the statistical properties of a light beam incident upon it! It has appeared online at Springer’s site and will be “officially” published later this year.
I don’t often talk about my own research on this blog… heck, I don’t think I’ve ever talked about my own research here, come to think of it! I thought it would be a nice change of pace to describe a paper that recently appeared in the journal Plasmonics of which I am a co-author. The paper, titled, “Coherence converting plasmonic hole arrays”, describes how one can use an array of subwavelength-size holes in a thin metallic screen to alter the statistical properties of a light beam incident upon it! It has appeared online at Springer’s site and will be “officially” published later this year.
For those not familiar with optics, there’s a lot to unpack in even the title of the paper: What is “coherence”? What is a “plasmon”? Why do we care about “converting” coherence? Let’s take a look at each of these ideas in turn as we build an explanation of what my collaborators and I have accomplished!
Let’s start with a short review of what we mean by optical coherence. Light has long been known to possess wave properties, and like all waves it can generate interference patterns: alternating regions of high and low intensity. The archetypical example is produced in Young’s double slit experiment, in which light is transmitted through a pair of slits in an opaque screen. The light emanating from the two slits interferes and produces a pattern on a secondary screen further “downstream”.
If the experiment is prepared correctly, one sees alternating bands of light and darkness on the second screen, as shown in a simulation below.
However, if one does this experiment with an ordinary light source, like a light bulb, the interference pattern will almost certainly not be seen. The reason for this is that a light bulb produces light that has different wave vibrations at different points in space — the light reaching the two slits in Young’s experiment are uncorrelated, or spatially incoherent. A crude illustration of the difference between correlated and uncorrelated waves is shown below; basically, correlated waves are doing the same thing, and uncorrelated waves are “doing their own thing”.
We can only get interference patterns by the interference of light from highly spatially coherent sources, such as a laser or a conventional source which has been appropriately collimated and filtered.
The propagation characteristics of light strongly depend on its spatial coherence. In addition to interference effects, the spatial coherence affects the directionality of light. A coherent laser beam, for instance, creates a beam of light that is essentially in a single direction, whereas a light bulb radiates in almost every direction. There are applications where it is useful to have light which is partially coherent: highly directional, but not able to produce strong interference patterns. For instance, it has been shown that partially coherent light will propagate through atmospheric turbulence with less distortion than a comparable fully coherent beam, making partially coherent beams potentially useful for free-space optical communications systems. Any technique which allows us to modify the spatial coherence of light would therefore be an excellent tool.
This is where surface plasmons come in! Speaking technically, a surface plasmon is an electron density wave that can be excited along the surface of certain metals by light. This is illustrated schematically below.
The “+” and “-” represent lower and higher densities of electrons along the surface, respectively, and the “E” and “H” represent the directions of the electric and magnetic fields. (The right-most figure crudely illustrates how the intensity of the surface plasmon is maximum at the surface and decays away rapidly away from it.)
A plasmon is an electron density wave, which means the thing that oscillates and travels along the surface of the metal is the highs and lows of the density of electrons. This is quite analogous to the behavior of sound waves, in which the density of the air molecules is “waving”.
There are a number of important aspects of surface plasmons (to be referred to simply as “plasmons” from now on) that make them very useful for optics applications. First, plasmons have a shorter wavelength, and consequently higher momentum, than the light that excites them. This means that plasmons cannot be excited on a smooth metal surface, but only at bumps or holes on that surface. Also, once excited, those plasmons will carry energy along the surface until they are either absorbed or hit another hole and get converted back into light. Second, plasmons are coherently excited at one of these holes or bumps, which means that there is a perfect correlation between the light illuminating the hole and the plasmon wave that gets generated.
Around 2007, my postdoc advisor started to think that these surface plasmons could change the state of coherence of a light wave. How would this work? Let’s look at a cartoon version of Young’s double slit experiment, and imagine that each slit is illuminated by an independent light beam. Therefore one hole is illuminated by “apples”, and the other by “oranges”.
The “apple light” and the “orange light” cannot interfere, and after passing through the holes, that hasn’t changed — no interference pattern will be created.
But now let us suppose that the screen with the slits can support surface plasmons. When the apple light hits the slit, part of it will be directly transmitted through the hole, but some of it will convert into a surface plasmon. This “apple plasmon” will travel to the other hole, where it will convert back into apple light! A similar argument applies for the orange light, and the result is illustrated below.
The light going into the pair of slits was completely uncorrelated (apples & oranges), but the light coming out of the slits is now correlated — apple/orange & apple/orange! By essentially swapping a part of the light between the two slits, the spatial coherence of the light has been increased.
My collaborators and I published a theoretical paper¹ on these results in 2007, titled, “Surface Plasmons Modulate the Spatial Coherence of Light in Young’s Interference Experiment.” In this work, we demonstrated that, depending on the separation of the slits and the wavelength of light, the spatial coherence of light could be increased or even decreased on passing through the pair of slits. The increase in spatial coherence was demonstrated experimentally and published later that same year.²
This work got me thinking: is it possible to change the spatial coherence of an entire beam of light using surface plasmons? In the plasmonic double slit experiment, we are only changing the spatial coherence of light at two points of a beam of light — the rest of the light is being blocked by the metal screen.
The natural thought was to imagine transmitting light through an array of holes in a metal screen.
When this array is illuminated by a beam of light, plasmons will propagate back and forth between multiple holes, and the light emanating from the collection of illuminated holes will presumably form a beam of light that has a modified state of coherence. But will it work?
Studying the interactions of plasmons bouncing around between multiple holes on a metal surface requires rather complicated numerical simulations, and things cannot be done with simple pen and paper calculations. As an intermediate step, my student Choon How and I studied³ the behavior of surface plasmons in Young’s three slit experiment!
The big question in the three slit study was whether the middle slit would hinder the propagation of plasmons to the outer holes. That is: can plasmons from the left hole “jump” the middle hole and influence the right hole?
It was found via simulation that plasmons do indeed jump the middle hole, and that the presence of the middle hole could help enhance the coherence between the outer holes. This opened the door to studying how the overall coherence of a beam of light could be enhanced by an array of holes in a plasmonic screen.
Every researcher eventually runs into an annoying project that just takes forever to get completed and written up. This study of a “coherence-converting plasmonic array” was such a project for me, and it took roughly 3 years to get it submitted for publication. It turned out to be difficult in large part for two reasons: 1. the complexity of the simulations, and 2. the challenge in defining the “overall” coherence of a beam of light.
In general, it can be tricky to perform exact simulations of the interaction of light with matter. The multi-hole plasmonic array we were interested in turned out to be a particularly difficult system to model, and in fact exact simulations were beyond the computing capabilities I had available at the time. However, it turned out that the exact results of the double slit and the triple slit cases could be reproduced quite accurately with a “toy model” of the system. For the double slit case, this toy model really involved treating the light propagation as consisting of the two parts described above: direct transmission through the slit and slit-plasmon-slit coupling. We implemented a similar model to study the interaction of light and plasmons for an array of holes; we were partially justified by the fact that others had done essentially the same thing to study different plasmonic systems.
Defining the “overall” or “global” state of coherence of a light beam also turned out to be somewhat of a challenge. Spatial coherence is usually characterized between two points in a light wave, as for instance the coherence between the light emanating from the two slits in Young’s experiment. Though it is clear that some light beams are more coherent than others (a laser produces light more coherent than a light bulb), quantifying this overall coherence has never been done satisfactorily. In the end, we opted to simply look at the coherence of light emanating from multiple pairs of holes in the array; if the coherence of most or all pairs increased/decreased dramatically, it was a good sign that the overall coherence had been modified.
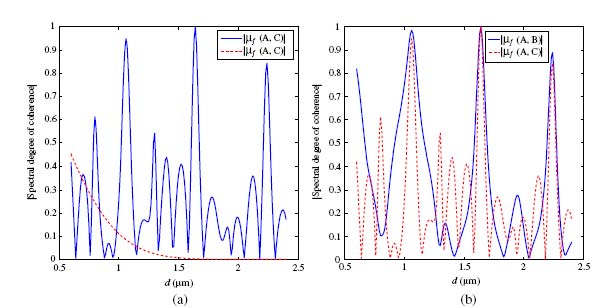
We studied 3 by 3 hole arrays, 4 by 4 hole arrays, and a 7-hole hexagonal array. We looked at how the degree of coherence of light emanating from the holes, called , changed as a function of hole separation
. A sketch of the hexagonal array, and the coherence results for that hexagonal array, are shown below.
The left figure above shows the degree of coherence — 0 for completely incoherent, 1 for fully coherent — between the holes A and C as a function of the array spacing , and compares it to what the degree of coherence would look like in the absence of plasmons (dashed line). It can be seen that for certain hole separations, the spatial coherence increases dramatically. In the right figure, we see the degree of coherence compared for holes A and B and for holes A and C as a function of array spacing. It can be seen that, for certain values of
, the coherence increases dramatically for both hole pairs; this is an indication that the transmitted beam as a whole has had its coherence increased! For instance, at hole separation 1.1 μm, 1.6 μm and 2.2 μm, both coherence values spike sharply, almost to full coherence!
We learned a few things from the simple simulations done in this research project. First and foremost, we found that we could in fact change the global state of coherence of a light beam by the use of a plasmonic hole array. This puts me one step further to my goal of designing “coherence converting plasmonic devices”, which could be attached to the front of a light source to change its statistical properties for various applications. We also noted that, unlike the two slit and three slit cases, there does not seem to be a hole separation that results in a global decrease in coherence. For some hole separations, the coherence between particular pairs of holes can be lower than the illuminating light, but we found no unique values of for which all holes exhibited a decrease in coherence. This may change, however, if we use more complicated hole arrangements.
Future research will involve the development of exact numerical simulations of the plasmonic systems in question, as well as investigations of more complicated hole arrays.
This work is also a good example of why it is important to diversify one’s research interests. I had developed a strong independent backgrounds in the theories of optical coherence and surface plasmons; this made it very easy to combine my knowledge to study the coherence of surface plasmons, a topic that nobody else had investigated before!
*******************
¹ C.H. Gan, G. Gbur and T.D. Visser, “Surface plasmons modulate the spatial coherence in Young’s interference experiment,” Phys. Rev. Lett. 98 (2007), 043908.
² N. Kuzmin, G.W. ‘t Hooft, E.R. Eliel, G. Gbur, H.F. Schouten and T.D. Visser, “Enhancement of spatial coherence by surface plasmons,” Opt. Lett. 32 (2007), 445.
³ C.H. Gan and G. Gbur, “Spatial coherence conversion with surface plasmons using a three-slit interferometer,” Plasmonics 3 (2008), 111.
*******************
Gan, C., Gu, Y., Visser, T., & Gbur, G. (2012). Coherence Converting Plasmonic Hole Arrays Plasmonics DOI: 10.1007/s11468-011-9309-1












Stuck in traffic and reading this, pretty interesting.
Thanks!
Hmmm. The thought of using plasmonics to modify coherence had never occurred to me, so I found this very interesting. Talks and articles about plasmonics always get me feeling as if there’s a spectacular research idea in the back of my head that I can’t quite drag up to the conscious level. Hmmm.
Even though I can follow your original papers (for suitably small values of “follow”), it’s always nice to see research written up at a more accessible and informal level.
Thanks! I tend to avoid writing about my own work, but I thought this was a suitably interesting result to describe.
Sweet stuff 🙂
Any way to test this without the ‘bumps and grooves’ of matter?
A electron density can be presumed without a metal too, as I understand?
Can one make a electron density field in air?
Or in a vacuum?
Not quite sure what you mean! It’s well known both experimentally and theoretically that plasmons & light only couple on surfaces with some sort of roughness.
A electron density can be presumed without a metal too, as I understand?
Can one make a electron density field in air?
Or in a vacuum?
Surface plasmons only appear in materials with the right dielectric and conductive properties. These properties mostly appear only in metals over a limited range of frequencies. Can’t do it in vacuum — there’s nothing there, including electrons!
I can imagine that building the simulations was quite challenging. Similar sorts of studies of distance dependence in geostatistics can be fiendishly difficult to calibrate and perform.
The simulations weren’t *too* bad, as the system was a relatively simple one. However, the problem had to be solved “self-consistently”, so that one takes into account all of the multiple interactions possible between light and plasmons. Also, we had to determine certain fitting parameters for the simulations by other means, and the results crucially depended on those parameters!
Ouch.
You’re right.
Didn’t think there, it was/is met wondering if ‘fields’ could interact.
But they can’t, can they?
Not in a vacuum.
It’s only in interactions with matter then.
But then again?
Free electrons in a vacuum, with a EM field directing them exist, doesn’t it?
And electrons have a rest mass.