Einstein’s special theory of relativity is arguably the most amazing physical theory ever conceived.  It utterly transformed our view of the universe, completely eradicating the view that space and time are independent quantities and giving us a new unified fabric of space-time.  It led us to the revelation that energy and mass can be converted into one another, and resulted in the world’s most famous physical equation,

,

which tells us that a mass m, times the speed of light c squared, is equivalent to (and can be converted into) an amount of energy E.  This observation forms the basis of nuclear energy, and it paved the way to all of modern particle physics such as the experiments being done at the Large Hadron Collider.

Perhaps the most fascinating thing about Einstein’s special relativity is that it leads to a collection of “paradoxes” that seem to violate our common-sense nature of the world.   Resolution of these false “paradoxes” demonstrate that the theory is wonderfully and incredibly consistent — and the best part is that many can be resolved using at most high-school algebra.

There are a variety of seeming contradictions in special relativity that turn out to be quite the opposite: the most famous of these is the “twin paradox“, in which one twin brother does a round trip to a distant star at high speed and returns to Earth, and there is a discrepancy in the ages of the twins when they return.

I’ve talked about the “twin paradox” in the context of another post; I thought for this one I’d discuss another unusual aspect of special relativity.  If you know anything about relativity, you probably know that it implies that nothing can go faster than the speed of light, which happens to be

.

In fact, the only thing that we know that can even match the speed of light is light itself!  As far as we know at this stage, no massive particle can achieve c, though it can come arbitrarily close to that speed.

With that in mind, if you were to jump into a rocketship and blast off to Alpha Centauri, which is 4.37 light years away from Earth, what is the fastest possible time that it could take you to get there with the fastest spaceship possible?

A natural first guess would be to say it would take approximately 4.37 years, since I can go no faster than the speed of light.  In fact, however, it turns out that with a fast enough spaceship, you could get to Alpha Centauri in as little time as you like — even 10 minutes or less!

How is this possible?  In explaining it, we will have to probe to the heart of two fundamental and surprising results from Einstein’s theory: time dilation and length contraction.  An important piece of the puzzle is noting that I asked how long it takes you to get to Alpha Centauri, not how long someone on Earth says it takes for you to get there…

All of special relativity derives from two fundamental postulates, first laid out by Einstein in his classic 1905 paper (in a slightly different but equivalent form).  These postulates may be stated as:

• Postulate of relativity.  The laws of physics are the same for any observer moving at constant speed.
• Invariance of the speed of light.  The speed of light is the same for all observers, regardless of the observer’s own state of constant motion.

The first postulate is an extension of the traditional statement of relativity by Galileo Galilei!  Galileo noted that a person traveling at the interior of a ship moving in calm seas at constant speed would not be able to detect that motion.  From this, Galileo deduced that the laws of physics were insensitive to motion at a constant speed.  In other words, no experiment can detect “absolute” motion — we play by the same rules of physics regardless of how fast we move.  In Galileo’s day, there were no systematic laws of light, electricity or magnetism formulated, and relativity was only applied to laws of force and momentum: Einstein extended the postulate by arguing that the laws of electromagnetism are also independent of constant motion.

The second postulate is the revolutionary one, but is closely related to the first. Early researchers believed that the speed of light would vary depending on one’s motion through space.  Because the speed of light is derived from the laws of electromagnetism, it followed that the physical laws of electricity and magnetism must change depending on one’s motion.  Einstein instead suggested that all of the laws of physics must be the same for all observers: the speed of light must therefore be the same for all, regardless of how fast an observer is moving himself/herself!

To appreciate how truly strange this is, consider the following thought experiment: imagine two cars (labeled 2 and 3) driving down the highway in opposite directions at 55 mph, as seen by a third car (labeled 1) stalled by the side of the road.

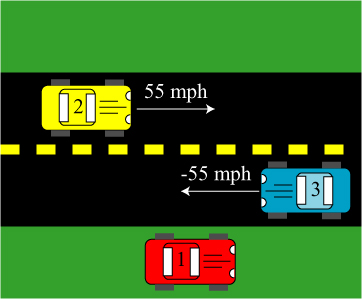So car 1 sees car 2 moving at 55 mph to the right (+55 mph), and sees car 3 moving at 55 mph to the left (-55 mph).  What do things look like for car 2 and car 3?  Car 2 sees car 3 approaching at 110 mph to the left (-110 mph), while it sees car 1 coming towards it at 55 mph to the left (-55 mph).  Car 3 sees car 2 coming to the right at 110 mph (+110 mph) and sees car 1 coming to the right at 55 mph (+55 mph).

That is the essence of Galilean relativity.  But now let’s imagine that there’s a beam of light shining down the road, illuminating all three cars, and all three cars measure the speed of the light.

So what measurements do the various cars make of the speed of light?  Well, by analogy with the example above, you might assume that car 1 measures c, car 2 measures c + 55 mph (because it is driving towards the light), and car 3 measures c -55 mph.

However, you would be wrong!  All 3 cars measure the speed of the light as c!  This is what is meant by the invariance of the speed of light — all observers measure the vacuum speed of light as c, regardless of their motion.

This constancy of the speed of light was first discovered in 1887 by Albert Michelson and Edward Morley, in a famous experiment that now bears their name (discussed at the end of this post).  The experiment was designed to detect variations of the speed of light due to the motion of the Earth in orbit around the Sun; no such variation was found, though it should have been readily observable.  It is unclear whether Einstein knew of this result when he formulated his special theory (there seem to be conflicting accounts from Einstein himself), but the constancy of c became a fundamental ingredient nevertheless.

How can we understand this very odd set of observations?  By understanding that, at very high relative speeds between observers, they will no longer agree on the same measures of time and space!

Let us consider a simple experiment that is occurring on a spacecraft traveling at a velocity v past an observer stationed on the Earth.  A laser beam is fired across the width of the spacecraft to a mirror a distance L away; the beam returns to the gun and the total round-trip time is measured.  The point of view of the experiment via a person on the craft and on the Earth is illustrated below: because the spacecraft is moving, the Earth observer sees the light beam follow a diagonal course to and from the mirror.

Now we ask the question: how does the round-trip time Δt measured by the person in the spacecraft compare to the time Δt´ measured by the person on Earth?

We can do some algebra to determine the answer, but I’ll relegate that messiness to an appendix to this post.  We will simply note the following: the Earth and spacecraft observers have different opinions on the distance the light travels.  Light travels a longer distance according to the Earth observer.  However, both of them measure the same value for the speed of light: this means that the Earth observer records a longer round-trip time than the spacecraft observer.

This is the essence of what is known as time dilation, and is often simply stated as: “time proceeds slower in moving clocks”.  In equation form, time dilation may be expressed as

.

Remember that Δt is the time interval measured by the spacecraft observer and Δt´ is the time interval measured by the Earth observer.  The quantity in the square root is always less than or equal to one, and it rapidly approaches zeros as v approaches c, the speed of light.

To see how this works, let us suppose our spaceship heads to Alpha Centauri at 90% of the speed of light.  According to the Earth-bound observer, the trip should take 4.86 years.  According to the person on the spaceship, however, the trip takes only 2.12 years!

This is quite surprising — according to our argument, it seems that the spaceship pilot can reach Alpha Centauri in less time than it would take light.  At first glance, it would seem our spaceship is traveling faster than light, since it travels 4.37 light-years in 2.12 years.  However, what in fact happens is that the distance to Alpha Centauri becomes shorter for the person in the spacecraft.

This can be shown to be true by another experiment with light (discussed in this post), as done above for time dilation, but we can argue it in a much simpler way as follows.  One other thing that the Earth observer and the spaceship observer must agree upon is the relative speed between them.  If the Earth observer sees the spaceship fly away at speed v, the spaceship observer sees the Earth recede at speed v.  Let us suppose that the distance between Earth and Alpha Centauri, as measured by Earth, is Δx´, and we refer to the distance between Earth and Alpha Centauri as measured on the spaceship as Δx.  Because speed is distance over time, the velocities can be written as

.

But we already know the relationship between Δt and Δt´, from our time dilation discussion.  Using time dilation in the above equation, we find that

.

Remember that Δx´ is the Earth-Alpha Centauri distance as measured from Earth, and Δx is the distance as measured from the traveling spacecraft.  Thanks to the square-root factor, we find that the person on the spacecraft sees the distance between Earth and Alpha Centauri as dramatically shorter!  How short?  For a spacecraft traveling at 90% of the speed of light, the distance will only be 1.90 light-years, less than half the distance that an Earth-bound observer would measure!  This is illustrated below: by any measurement the spacecraft observer can make, the distance between Earth and Alpha Centauri — and the planets and stars themselves — appear squashed!

This warping of space and time is the most shocking part of special relativity when one encounters it for the first time.  It is important to note that I use words like “perceive”, “observe” and “point-of-view” to describe the changes in time and space, but these are real changes — no physical experiment or measurement of any kind will disagree with the results.  It is also important to note that time is not “slowed” on the spaceship — the passengers experience time normally, but they simply observe (note the use of that word again) that the journey takes much less time, and is spatially much closer, than it would appear to require on Earth.

This argument can be taken to a logical extreme — if we could build a fast enough spaceship, its passengers could travel an arbitrarily far distance in as short a time as they like, say 1 million light-years in 10 minutes!  The major caveat to this, however, is during that 10 minutes, 1 million years would pass on Earth — there would be no going home!

There is another limit to this travel, however, that is based in Einstein’s general theory of relativity.  Thanks to observations of light from distant stars, scientists have confirmed that space itself is stretching and growing, in what is known as the metric expansion of space.  The most distant parts of the universe are in fact effectively moving away from us faster than the speed of light thanks to this stretching — these regions cannot be reached no matter how fast we move towards them.  Imagine trying to run across a huge sheet of rubber that is being stretched by people who are running away very fast on either end.

It is almost frightening how well special relativity works, and how internally consistent it is.  The simple arguments presented here don’t do full justice to how smoothly the concepts of space and time are intertwined in the theory, and how much sense this link makes on close inspection.  We can note, however, that the constancy of the speed of light is well-established experimentally (starting with the aforementioned Michelson-Morley experiment), and in fact time dilation has been confirmed experimentally almost countless times!

The most noteworthy of these experiments involves the use of cosmic-ray muons, elementary particles that are created in the upper atmosphere of the Earth.  The muon, a heavy version of the electron, decays when at rest (not moving) in around 2 millionths of a second.  If time dilation did not occur, almost none of these muons would survive to reach the Earth’s surface, but in fact we see an abundance of them — and in amounts in perfect agreement with special relativity.

Curiously, length contraction has never been measured directly! In order to observe length contraction, we would need to either measure the length of an object of significant size while moving close to the speed of light or, equivalently, measure the length of an object which is moving close to the speed of light itself.  Considering the space shuttle only reaches a top speed of 3094 mph (or 0.0005% the speed of light), we can’t observe length contraction directly.  However, as we have seen, length contraction is more or less implied by the existence of time dilation and the constant speed of light.

There is plenty more that can be said about the oddness of special relativity.  For instance, if you’ve been thinking about it carefully, you might ask: “Why does time dilate for the person on the spaceship, and not for the person on the Earth?  From the point of view of the spaceship observer, it is the Earth that is moving fast, not the spaceship.”  This is in fact absolutely correct — excluding some subtleties, we know that while the spaceship is in transit each observer sees the clocks of the other observer running slow!  How can each person consistently see the other’s clock run slow?  That will have to be a topic answered by another post…

*********************

Appendix: time dilation formula derivation

We’ll need to do a little algebra to make sense out of the two different observers on the Earth and on the spacecraft.  For the observer on the spacecraft, the light travels a total distance 2L at a speed c; the total time it takes for the light to make its round trip is

.

But what does this experiment look like from the point of view of the Earth observer?  We call the round trip time for this observer Δt´, and we note that during this round trip the spacecraft must travel a horizontal distance

.

In order to keep up with the moving mirror and the laser gun, the light beam follows a diagonal trajectory with side length D; use of the Pythagorean theorem tells us that D has the value

.

We also know, however, that the total round trip time must satisfy

.

Substituting this into the first expression for D, we have

.

With some algebraic manipulation, we may write

.

But remember that Δt is just 2L/c, so we may write

.

This is the time dilation formula!  The observer on Earth sees a time interval Δt´ which is longer than the time interval seen on the spaceship, Δt.