Since the first theoretical cloaking papers in 2006, the topic of optical invisibility has just gotten stranger and stranger. There have been proposals of optical wormholes, perfect optical illusions, space-time cloaks, and more. Perhaps even more surprising, however, is the speed at which practical implementations of a number of ideas have been achieved. Consider, for instance, this short video of a macroscopic optical invisibility cloak, a small-scale version of an object demoed at TED 2013 by physics professor Baile Zhang:
Impressive, is it not? This device is the implementation of a cloaking idea introduced in 2008* and described colorfully as “hiding under the carpet!” It holds the most promise in the short term for being able to effectively hide macroscopic (larger than microscopic) objects.
But what is a “carpet cloak,” and how does it work? To answer this, we delve back into the weird optics of cloaking devices, and their design using theoretical warpings of space!
A “carpet cloak” is an optical device that sits above a region of space and makes that region appear flat and empty, regardless of what lies underneath it. This picture below illustrates roughly how this works for rays of light: the rays get deflected while in the carpet but return to their original trajectory as if they had hit the flat surface unobstructed, or passed by it.

Illustration of the carpet cloak concept. The dashed lines indicate the paths of rays in the absence of the cloak and object.
The object is concealed by hiding it underneath the cloaking device, much like cats like to hide underneath blankets, comforters or carpets; hence the name “hiding under the carpet.”
How does a carpet cloak work? The speed of light in matter is typically characterized by a quantity known as the refractive index that, loosely speaking, is the fraction by which the speed of light slows in matter. For instance, if the speed of light in vacuum is labelled c, the speed of light in a material is given by c/n, where n is the index. For air, the refractive index is approximately 1, for water, the refractive index is about 1.33, and for many types of glass the index is about 1.5. A refractive index higher than 1 is a speed slower than the speed of light, and an index lower than 1 is a speed faster than the speed of light.
When light travels in a material with a spatially-varying refractive index, its path gets deflected, typically being bent from the region of low index to the region of high index — the light “wants” to go slower! If we design the material properties of a carpet cloak just right, we can get the light to bend away from the hidden region to form a quite convincing illusion.
The next question to ask is a practical one: how do we come up with a design for this carpet cloak? The trick that makes it possible to do so is a bit of mathematics now known as transformation optics. In short, researchers noted that light traveling in certain types of transparent media acts mathematically the same as light traveling through a warped region of space. If we can imagine a warped region of space that meets our goals, we can determine the material that will produce the same effect. This is best illustrated with the original cloaking designs introduced in 2006, which I have blogged about in detail previously.
Restricting our attention to the design of Pendry, Schurig and Smith, the cloak is spherical and hides a spherical region within its interior. Light coming from any direction is guided around the interior and sent along its original path, as shown in their original illustration.
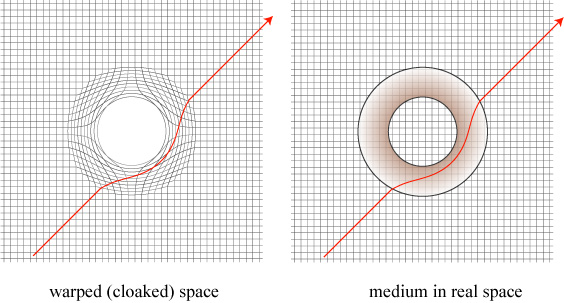
So what kind of warping of space will bend light rays away from a spherical hiding place? Let us imagine that we have an ordinary region of space, illustrated by a rectangular mesh on a sheet of paper (or rubber, which can be stretched). We poke a point-like hole in that paper and stretch that point into a circular hole, as illustrated below.
The red line indicates a ray of light passing near the cloaked region. As the space is stretched away from the point, so are rays bent away from the hidden region. The region where the mesh is distorted can then be simulated by a complicated spatially-varying optical material, as illustrated below.
Seems simple enough — well, at least simple to explain! However, actually fabricating the materials to make such a cloak work for visible light — light that we can see — is extremely difficult, and in fact is currently impossible.
We can gain a partial understanding of the difficulties involved by looking more closely at the warped space picture above. What happens to a wave traveling through a region of warped space? Below we draw a picture of a single-frequency wave traveling horizontally from unstretched into stretched space:
 The wavelength of light — the spacing between the peaks of the waves — gets bigger in the stretched region. However, a longer wavelength implies a faster wave velocity! Waves go faster in stretched space, and slower in squashed space. We can therefore say that the spacing of the lines in our warped space pictures is proportional to the speed of the wave.
The wavelength of light — the spacing between the peaks of the waves — gets bigger in the stretched region. However, a longer wavelength implies a faster wave velocity! Waves go faster in stretched space, and slower in squashed space. We can therefore say that the spacing of the lines in our warped space pictures is proportional to the speed of the wave.
What happens if we take the same stretched space and send a wave vertically? In the vertical direction, there’s no stretching, and the wave speed doesn’t change. However, this implies that the speed of light is different in different directions: the warping is equivalent to a medium which is said to be anisotropic.
Most materials in nature are isotropic: the speed of light is the same regardless which way the light is going. A good example of an anisotropic material is optical calcite, which produces two images of objects viewed through it.
Though a discussion of how exactly two images are formed is more complicated than we want to get into right now, suffice to say that we get two images because of two different speeds of light in the medium.
Now we can look again at our spherical cloak, shown below.
Square A is outside the cloak, and represent ordinary, isotropic space. Shapes B and C inside the cloak represent anisotropic regions of the cloak, because the shapes are not square. This cloak is therefore anisotropic, and the anisotropy depends on the distance from the center, as shapes B and C are different from one another — it is spatially varying. Notice that the shapes get taller and narrower as we get to the edge of the inner cloaked region. We can’t see it exactly from this picture, but if we had a fine enough mesh we would find that the speed of light gets arbitrarily large at that edge, i.e. the refractive index goes to zero!
So from a manufacturing perspective, we need to make a material that is anisotropic, spatially varying, and has the speed of light infinite on the inner boundary. The first two conditions are simply not possible with current technology; in the future, we may be able to construct metamaterials which can do it, but not now. The infinite speed limit is a much bigger problem: it is possible to have the speed of light in matter be infinite at a single frequency (color), but not over a range of colors. Even if we can figure out how to make the materials to build a spherical cloak, then, we would only be able to make it invisible to, say, red light!
These concerns motivated the introduction of the idea of carpet cloaking. It is possible to make a carpet cloak that has very little anisotropy and reasonable values of the refractive index. There are many warpings of space that can make a carpet; one of the possibilities is shown below.
We can see from this picture that the anisotropy, and the spatial variation of the cloak, are minimal: the boxes are all pretty close to square and roughly the same size. Furthermore, the refractive index variation is pretty small: the boxes in the cloak are all approximately the same size as the boxes outside. In fact, it is possible to distort the boxes even more to reduce the anisotropy further, though at the expense of an increased variation of the refractive index.
It is therefore much easier to make a carpet cloak, and it didn’t take very long to make it happen. The first result was published in April 2009 by Valentine, Li, Zentgraf, Bartal and Zhang**, who made a cloak that functions for near-infrared wavelengths, very close to the visible; however, the cloaked region was only 400 nanometers (400 billionths of a meter) high. Results were published soon after in July 2009 by Gabrielli, Cardenas, Poitras and Lipson, concerning a device of similar dimensions and also operating in the near-infrared. A third example was introduced by Ergin, Stenger, Brenner, Pendry and Wegener in 2010****, also functioning in the near-infrared but effective over a large range of frequencies.
All of these devices, as the numbers above indicate, only cloak very small regions and none of them work for visible light. In essence, these cloak designs are still too complicated to build on a scale beyond the microscopic. But suppose we made a triangular gap instead of a curved one to design our cloak, as shown below?
Now, dividing the cloak with a vertical line down the middle, each of the squares on either side are identical: this cloak is anisotropic, but has uniform optical properties on either side — and in fact the optical properties are simply mirror images of each other. Now we don’t need a complicated spatially-varying material to make the cloak — if we can find a natural anisotropic material, it can be cut into two pieces and fashioned into a cloak.
It turns out: optical calcite, mentioned and pictured earlier, works perfectly.
In 2011, Zhang, Luo, Liu and Barbastathis***** fashioned such a carpet cloak by putting two pieces of optical calcite together. The resulting cloak works for visible light, and therefore can produce spectacular invisibility illusions like in the video shown at the beginning of the post.
Though an impressive illusion, there are a number of limitations to the calcite approach. First, in order to get “perfect” invisibility, one needs to have a material with magnetic properties. Optical calcite does not have such properties, and therefore it possesses reflections that make the cloak itself quite visible. It can hide objects underneath it quite well, but it can’t hide itself!
Second, the device as shown above only works from a limited range of viewing angles. It is not an accident that the video only shows the cloak operation directly from one side. Looking from one of the sides not shown, or from the top, will also break the illusion. In principle, a carpet cloak can be made which hides from all directions, but with just two pieces of calcite it cannot..
Third, scaling this up to a bigger size is possible, but only to a certain extent. Calcite, like all materials, absorbs some fraction of the light passing through it. For a bigger cloak, light will have to travel farther through the calcite and will be attenuated more. This also will make it visible, as the cloak will effectively cast a small shadow.
This carpet cloak, however, shows that it is difficult to predict what can be accomplished in optical invisibility. Even four years ago, it seemed that an invisibility cloak of any kind operating with visible light was decades away, if not impossible. Now we have a working prototype. I suspect that we still have quite some time before we have to worry about true science fiction-style invisibility, but Zhang’s carpet cloak makes me hesitant to make any bold declarations. It is wise to keep one’s opinions on future developments cloaked, it seems!
***************
* J. Li and J.B. Pendry, “Hiding under the carpet: a new strategy for cloaking,” Phys. Rev. Lett. 101 (2008), 203901.
** J. Valentine, J. Li, T. Zentgraf, G. Bartal and X. Zhang, “An optical cloak made of dielectrics,” Nature Materials 8 (2009), 568-571.
*** L.H. Gabrielli, J. Cardenas, C.B. Poitras and M. Lipson, “Silicon nanostructure cloak operating at optical frequencies,” Nature Photonics 3 (2009), 461-463.
**** Y. Ergin, N. Stenger, P. Brenner, J.B. Pendry and M. Wegener, “Three-dimensional invisibility cloak at optical wavelengths,” Science 328 (2010), 337-339.
***** B. Zhang, Y. Luo, X. Liu and G. Barbastathis, “Macroscopic invisibility cloak for visible light,” Phys. Rev. Lett. 106 (2011), 033901.











Liked the article. Could you elaborate a little more on what you mean by “it is possible to have the speed of light in matter be infinite at a single frequency (color)?”
Thanks! Yes, I need to elaborate on that a bit more in a future post, but I can say a few words here. The refractive index of matter is frequency-dependent, and therefore depends on the frequency or color of light passing through it. When a pulse of light with many frequencies passes through matter, therefore, it gets distorted in a process known as dispersion. We can talk about the speed of light for each frequency independently, though, and that speed is just the vacuum speed divided by the refractive index at that frequency, c/n.
Now, Einstein’s special theory of relativity suggests that nothing can travel faster than the vacuum speed of light c, but one has to be careful in explaining what we mean by “nothing.” What we really mean is that it is not possible to convey information at a speed faster than c, but any disturbance that does not convey useful information can apparently break this rule. A classic example is shining a laser beam on the moon from earth. I can make the spot of light move across the surface of the moon as fast as I want by tilting the laser pointer, but no information gets conveyed from point A to point B on the moon by the moving spot, so there is no violation of relativity.
A single frequency wave can actually have an arbitrarily high speed as well, because a single frequency wave is in principle unchanging for all times, from the infinite past to the infinite future — it just keeps oscillating at that same frequency. No matter how fast those oscillations move through space, we can’t convey information on them, because if we were to try and encode the signal by distorting the wave, it would no longer be single frequency! Another way to say it is that a monochromatic wave is not causal — since it has no beginning or end, and is essentially the same at all times, it doesn’t break any rules for it to move as fast as it wants.
The speed of light at a single frequency is what we typically call the phase velocity, as compared to the group velocity and the signal velocity. The signal velocity is causal, and limited by Einstein’s relativity. I discuss the meaning of the three in this older post. Also, it is possible to make the group velocity faster than c, but this trick also does not involve breaking the speed of light c. Hope this makes sense!
Fantastic article, thanks for posting.
Thanks!