Is it possible to make something invisible in time as well as in space? It is a fascinating question, a provocative question, a mind-boggling question… wait… what exactly does it mean to “make something invisible in time?”
We’ll get to that, but it has in fact been done: several days ago, a group at Purdue University made world news when they announced a new and vastly improved experimental demonstration of a “temporal cloak.” Of course, “new and improved” implies that this has been done before, and it has: I blogged about the first realization of such a time cloak early last year. For those unfamiliar, however, it is worth spending some time explaining the principles behind it, and how this new version is a much simpler and more powerful design that could lead to practical applications in short order.
So what is a “temporal cloak?” Despite what the name may suggest, it is not a way to warp the fabric of time or “hide time,” whatever that may mean! The reality is much more mundane, but nevertheless fascinating: a temporal cloak is a way to create a moving gap in a continuous beam of light and stitch it seamlessly back together at the output, leaving the beam seemingly never broken to an observer. Anything passed in front of the beam within one of these gaps does not block or otherwise interact with the light: the object has been “cloaked” from the light!
This is an odd concept, so we should try and come up with an analogy to clarify things. In my previous post I described it in terms of a curtain factory; here let’s talk about a train crossing! Let’s imagine a train crossing where trains go by all the time, making the intersection almost continually blocked by moving trains. This, of course, is really annoying to passerby.
To solve the problem, they bring in an insane engineer who comes up with a really bizarre plan: make the train cars flexible in the middle! If someone approaches the intersection to cross, a pair of cars will uncouple, and the cars then compress, leaving a moving gap between them. A quick person can cross through the gap; then the cars expand again, linking back up some distance after the intersection. The train never slows down or stops and there is no break in the flow of the train outside of the crossing region.
This is, in essence, what a temporal cloak does for a continuous stream of light: inside the cloak region, a moving gap is opened in the beam which is closed before it exits. Anything that passes through the gap is not illuminated with light and therefore does not break or otherwise influence the steady beam of light. The event has been “cloaked.”
It is natural to ask at this point why such a device might be called a “time cloak” at all! I have previously discussed how the original cloaking schemes were designed by finding a material structure that is equivalent mathematically to a warping of space away from the cloaked region, as crudely illustrated below.
A few years ago, researchers realized* that such a transformation is also possible when one of the coordinate axes is replaced by time.
The picture is the same, but the interpretation is quite different! Rays above the warped region travel faster than the average speed to open a gap and then slower to close it; the converse happens for rays below the warped region. The design is essentially the same as for a more conventional invisibility cloak, but with one spatial position replaced by time: it is, therefore, known as a “temporal cloak.”
In 2012, researchers produced the first experimental demonstration** of a temporal cloak, using a device known as a “split-time lens.” Though it was a groundbreaking achievement, the amount of cloaked time was very small, amounting to 50 picoseconds (thousandths of millionths of a second) over a 24 microsecond interval. This means that, out of every 24 microseconds, only 0.0004% of the time could be hidden. For comparison, if this scheme were being used to hide events during a half-hour sitcom broadcast, the cloak would only be operational for 0.004 seconds!
The 2012 research was therefore a scientific first, but was not terribly practical. To use this scheme in any application, much more time would need to be hidden at a much faster rate. In coming up with a solution***, the Purdue research team looked for inspiration nearly 200 years in the past, and applied the Talbot effect to temporal cloaking!
First observed by Henry Fox Talbot in 1836, the Talbot effect is the curious self-imaging of light that passes through a periodic diffraction grating, as illustrated below.
Light coming from the left passes through a periodic array of holes and propagates along. As the intensity plot above shows, at certain distance, the light reconstitutes into a perfect image of the light intensity at the output of the holes themselves! The right-most image is the standard Talbot image, and the vertically-shifted image in the middle is known as the secondary Talbot image. Between these perfect reproductions are scaled copies of the original light distribution, which I talk about in an older blog post on the subject.
Suppose instead of making a periodic grating out of holes, we make it out of an array of converging lenses that focus the light instead of blocking it? Then we get a “Talbot carpet” that looks something like the image below.
Again, the light starts on the left, and travels to the right. The interesting thing is that, along the way, the traveling wave ends up with huge gaps where there is almost no light at all, represented by the dark regions of the plot. Any object placed in one of those dark regions will not effect the field at all, which will again be perfectly reproduced at the Talbot distance on the right side. Objects in those regions are “cloaked” from the Talbot light.
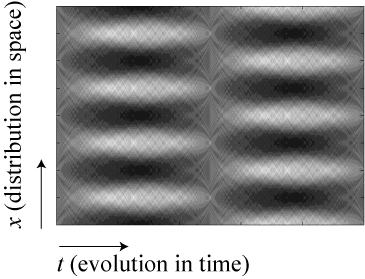
The Purdue research group took advantage of this, and also took advantage of the fact that it is possible to create a temporal Talbot effect. Mathematically, a steady-state light wave propagating in the z-direction with a transverse profile in the x-direction is equivalent to a light wave with a longitudinal profile in the x-direction and an evolution in time along the z-axis! This reinterpretation is very much analogous to the pictures above that show how an ordinary cloak can be reimagined as a temporal cloak by changing one of the axes to time.
So how would we interpret this plot in this case? At t=0 (left side), we have a continuous beam of light stretched out in space, and we apply a Talbot-like transformation to the beam. As time passes, this continuous wave separates into squeezed “clumps” of light, just like our train cars above squeeze into localized clumps of train cars. After a certain amount of time, call it the “Talbot time” (right side of plot), the waves automatically declump; we can then apply another transformation to them to undo the Talbot effect and, voila! We have a continuous undisturbed beam of light coming out of the system. Anything that happens at positions x and times t where the plot is dark does not have any effect on the light; those events are cloaked.
The use of this Talbot scheme allowed the researchers to demonstrate some truly impressive temporal cloak numbers: they were able to effectively hide 46% of the time axis at a rate of 12.7 GHz. This means that not only were they able to increase the rate of hiding — 12.7 billion hiding events per second, as compared with 40,000 hiding events per second in original experiment — but they were able to cloak almost half of the time. To use our sitcom analogy again, this means that nearly half of the sitcom would be hidden — albeit in a large number of very small chunks!
The method used here took advantage of existing technology that is currently used for generating a sequence of pulses and compressing them; the authors suggest that it may be possible to stretch this technology to achieve 90% time cloaking, a truly impressive feat and one that would not have seemed possible even last year.
So, um, what can we do with this technique? Looking over the results, I’m still not entirely sure of the practical applications. Continuing the train analogy from above, it might be possible to use temporal cloaking to seamlessly open up gaps in streams of data to mix them together, much like train cars are reorganized in a railroad yard. The ability to compress streams of information into very narrow and garbled pulses might also find application in new data encryption schemes.
The subtle challenge in application comes from the fact that temporal cloaking does not involve hiding data in a beam of light, it involves hiding data or events from a beam of light! For now, the applications of temporal cloaking are as well cloaked as the data it is being used to hide.
P.S.: I’m actually quoted in the BBC piece on this new cloak!
************
* M.W. McCall, A. Favaro, P. Kinsler and A. Boardman, “A spacetime cloak, or a history editor,” J. Opt. 13 (2011), 024003.
**M. Fridman, A. Farsi, Y. Okawachi, and A. Gaeta, “Demonstration of temporal cloaking,” Nature, 481 (2012), 62-65.
*** J.M. Lukens, D.E. Leaird and A.M. Weiner, “A temporal cloak at telecommunication data rate,” Nature (2013), doi:10.1038/nature12224.









Interesting, but talking about ‘time being stopped, or disappearing’ under some ‘time segment’ as described by a observer, imply that this is a effect between ‘frames of reference’ to me? How would I argue that it disappear for all frames of reference?
“Rays above the warped region travel faster than the average speed to open a gap and then slower to close it; the converse happens for rays below the warped region. ” Thinking of it as rays in a density, it makes sense? But I’m not sure what it has to do with time though?
If I would assume that the vertical lines represent a time they seem to indicate a arrow bending both forward and backward in time, all of it observed from the same observer? At the same time as he finds it to take certain (normal) time, measuring the time versus his local clock?
That last idea becomes logically inconsistent to me.