Over the years, there has been a lot of hype about the possibility of “superluminal” light: namely, light than can travel faster than the vacuum speed of light meters/second, which is overwhelmingly considered the absolute speed limit of the universe. I’ve talked about superluminal light before, and the related discoveries always turn out to be somewhat less spectacular than they sound, though they always provide some strange insights into the physics of light.
Recently, though, an even stranger discovery has been making the rounds in the press*: an experiment performed by researchers in Glasgow and Edinburgh** shows that appropriately-prepared light particles (photons) can travel even slower than the vacuum speed of light — in vacuum!
Kind of like its superluminal siblings before it, this discovery has caused a bit of confusion. In this post I’ll try and shed some light on the phenomenon, showing why it is both less and more than it appears.
Perhaps the first stage of our journey is to explain why this result seems so surprising at all! After all, light travels slower whenever it enters a transparent material. When it enters glass, for instance, light slows to roughly 2/3rds of its vacuum speed. In a vacuum, however, one of Einstein’s postulates of special relativity says that “The speed of light in free space has the same value c in all inertial frames of reference.” This seems to suggest that everyone, regardless of their motion with respect to a light source, measure exactly the same c — no more, no less. In a cursory reading of the popular accounts, it sounds like the Glasgow and Edinburgh experiment has violated this rule.
Let’s be clear, though, right off the bat: the vacuum speed of light c is a fundamental constant of nature, and remains so. Its value can be derived from, and in a sense is determined by, two other fixed fundamental constants in nature, the electric permittivity and the magnetic permeability. These two constants may be thought of as comparative measures of the strengths of the electric and magnetic forces. The “vacuum speed of light” as a fundamental constant is still something that everyone can agree on, regardless of their relative motion.
When looking at real beams of light, however, there is some subtlety in how we define their speed. I’ve talked about this in some detail in a previous post, and reiterate the highlights here.
The trick, as it is, is that light is not a solid object, and a pulse of light can change its shape as it propagates. This means that there is some ambiguity in how we actually define the its speed, as we typically define the speed of an object by dividing the distance it traveled by the time it took to travel that distance. But how to measure that distance? For a car, we can simply choose a fixed point, like the front bumper, to make all measurements.
When the moving object changes its shape, however, like a hurled bucket of water, there is no definite point to follow to measure distance! The overall speed of an object becomes ambiguous.
To solve this problem, physicists have introduced several different ways to quantify the speed of light. Continuing our water analogy, we can describe these speeds as shown in the picture below.
To measure the phase velocity, we look at individual droplets of water and choose one that represents the “typical” speed of the whole mass of water. To measure the group velocity, we consider the center of mass of the entire body of water and measure how fast that is moving. To measure the signal velocity, we consider the speed of the front end of the body of water. In terms of light, the signal velocity is the only velocity that cannot be greater than the vacuum speed c; this carries the implication that information cannot be conveyed faster than this speed.
In the experiment considered here, the group velocity was the quantity being measured. Using the word “group,” however, raises the question: group of what? It turns out that, theoretically, it is always possible to express any beam or pulse of light as a group of plane waves propagating in different directions.
A plane wave may be considered the simplest building block for constructing any light wave, sort of a LEGO building block for waves. An illustration of such a wave is shown below.

Illustration of the wavefronts of a plane wave. The “ups” of the wave, which form planes, are traveling to the left.
The wave shown here is traveling to the left, and the individual “wiggles” of the wave are traveling in this direction as well. The only variation of the wave is in the propagation direction, and if we color in all the points in space where the wave is “up,” we get a series of equally-spaced parallel planes.
Plane waves, as the fundamental building blocks of all optical waves, all travel at the vacuum speed of light c; in some sense, when we say “all light travels in vacuum at speed c,” that is really a shorthand way of saying, “the fundamental building blocks of light waves all travel in vacuum at c.”
So how can we add together two waves traveling at c and get a wave traveling at a speed less than c? The answer is ridiculously simple. Let’s imagine we just have two plane waves, traveling at opposing angles θ to the horizontal.
 Each plane wave, individually, is traveling at c along the angles θ; in what direction and at what speed is the group of two waves traveling? There is no net wave propagation along the vertical y-direction, as the upward flow of the one wave is perfectly canceled by the downward flow of the other. The only travel is in the z-direction, and because part of each plane wave’s velocity is along y, the speed along z is smaller! Another way to put it: the larger that θ is, the more that the group of waves is traveling along y and the less that they’re traveling along z.
Each plane wave, individually, is traveling at c along the angles θ; in what direction and at what speed is the group of two waves traveling? There is no net wave propagation along the vertical y-direction, as the upward flow of the one wave is perfectly canceled by the downward flow of the other. The only travel is in the z-direction, and because part of each plane wave’s velocity is along y, the speed along z is smaller! Another way to put it: the larger that θ is, the more that the group of waves is traveling along y and the less that they’re traveling along z.
It is, in essence, that simple. When we propagate a wave that consists of a collection of plane waves traveling in significantly different directions, the overall net speed — or group velocity — will be slower because each of the waves dedicates only part of its “allotment” of speed to travel along the group direction.
When we look at the structured light used in the experiment to slow light in a vacuum, we can see this clearly. One of the structured light fields used was a so-called Bessel beam, named such because it produces a transverse field pattern in the form of a Bessel function. The intensity of such a beam, head-on and magnified, would look something like below.
How does one form a Bessel beam? One simply combines a set of plane waves whose directions form a cone around the “group” direction of propagation!
The slowdown of the Bessel beam is essentially a more complicated version of our two plane wave example from earlier. The other structured beam considered in the Glasgow/Edinburgh experiment is a focused light beam.
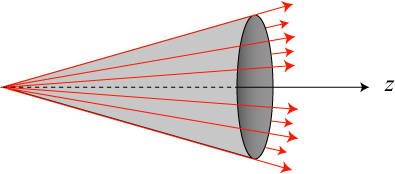
A lens essentially takes a single plane wave (or, if you prefer, a bunch of parallel light rays) and converts them into a set of plane waves lying within a cone that converge to a focal point. Though the rays near the center of the lens more or less travel in a straight line, the rays that enter near the edge of a lens are diverted significantly, and “spend” much of their speed traveling vertically.
This is what I meant at the beginning of the post when I said that this discovery represented a little less than it first appeared. There is no fundamental rewriting of Einstein’s relativity or even, in general, significant changes to the speed of light. It is really a geometric effect related to how the plane waves in a beam of light are distributed.
The result, as stated so far, could be said to be a correction of one of several common misconceptions that arise when you discuss the properties of light only in terms of the fundamental plane waves. For example, you might have heard the statement that “light is a transverse wave,” which is usually illustrated by a picture as follows.
The idea is that the electric field E and the magnetic field H both oscillate perpendicular to the direction that the wave is traveling; however, this is a statement that, like the speed of light, only strictly applies to plane waves. If we look at the electric field after focusing, we might see something like the following.
The red electric field vectors of the light before the lens are perpendicular to the direction of propagation. The lens, however, bends each plane wave, and the electric field vector of each plane wave bends to remain perpendicular. The total electric field near the focal point (in the box), will have vertical parts that cancel, leaving a horizontal electric field pointing along the overall group direction of propagation. When looking at a structured field, the statement “electric fields are transverse” is also in general not true.
In fact, the observation that the group velocity of light in vacuum can be smaller than c is not new, and was discussed (and argued) in some detail in the first years of the 21st century. So what is new about this experiment? In it, the researchers measured the speed of single photons that had been appropriately structured, and found that single photons are also slowed.
This may seem like a small point, but it is a significant piece in a larger discussion in optics on whether the rules that apply to classical light waves (with lots of photons) also apply to quantum light waves (with single photons). In 2011, I blogged about another experiment in which researchers tried to determine whether single photons could cheat and go faster than the vacuum speed of light — the answer, in that case, was negative. The Glasgow/Edinburgh collaboration demonstrated, however, that photons have no problem slowing down in a vacuum, if they are appropriately structured.
The last thing to do is explain briefly how this delay was measured! Simply being able to measure such short delays in light travel, on the order of 30 femtoseconds (30 millionth-billionths of a second), is quite an achievement. A simplified schematic of the experiment is shown below.
An ultraviolet laser pumps a nonlinear beta-barium borate crystal, producing two identical photons each of half the energy of the original photon. These two photons are divided at a wedge prism, and one is sent through a fixed length fiber optic line to the detector. The other is sent into a free-space propagation configuration: the first spatial light modulator (SLM) imparts the structure to the light, either Bessel or focusing, and the second SLM undoes that structuring after the beam has propagated through the air.
Since it is almost impossible to make an absolute measurement of the time a photon takes to travel over such a short distance, the delays were determined by a coincidence measurement using the Hong-Ou-Mandel effect***. Explaining this effect would be another post in and of itself, but in short: when two photons enter a beamsplitter at the same time, they tend to leave from the same side of the beamsplitter. With the coincidence detector only triggering when a photon arrives at two different detectors, the simultaneously arrival of photons is then detected by a drop in the measured coincidence. Calibrating their system for light which is unstructured, the experimenters then used the SLMs to structure the light, and determine how much delay needed to be removed, using the translation stage, to return the photons to simultaneous arrival.
It is unclear whether this result will have any long-reaching implications for optical experiments. When light travels a long distance, any structuring it has been given tends to be lost relatively quickly, meaning that the total delay of light in such a situation is finite and usually negligible. (This also explains why nobody had noticed such a thing before.) In the long run, however, it may turn out to be useful for people performing very sensitive quantum optics experiments involving ultrashort pulses.
There’s one other baffling thing to note about this experiment: Bessel beams, which were measured here to be subluminal, were originally claimed**** back in 2000 to be superluminal! It seems quite baffling that something moving slower than c could have originally been experimentally measured to be faster than c. The answer to how this happened is also very interesting and very subtle, and something I’ll try and explain in a future post…
******************************
* I’m actually quoted at the end of this particular article from Science News!
** Giovannini, Romero, Potocek, Ferenczi, Speirits, Barnett, Faccio, Padgett, “Photons that travel in free space slower than the speed of light,” arXiv.org. Nice thing to see: three of the authors — Romero, Speirits, and Faccio — are women!
*** Random personal trivia: as a grad student, I had an office across the hall from the late Professor Mandel, who was a pioneer in quantum optics.
**** Mugnai, Ranfagni and Ruggeri, “Observation of superluminal behaviors in wave propagation,” Phys. Rev. Lett. 84 (2000), 4830.









Helpful post – many thanks.
The constancy of the speed of light relative to the observer is disproved by Sagnac experiment and also by GPS.
wrong
Waves don’t travel (< travail < trepale) but go, fare, or wend; one travels on foot or by oar.
Glue is fast; motes are fleet; rockets are swift; birds are quick; pizza is speedy; deeds are hasty.
There is no "vacuum": http://en.wikipedia.org/wiki/Scharnhorst_effect.
The authors were not nice < niais < nescius := not-skilled to see.