A couple of weeks ago, after a glass of wine, I did a twitter “ask me anything” about optics and light which resulted in the question that is the title of this post.  I took a rough twitter stab at it that led to a spirited discussion with Dr. Matthew Francis, at the end of which I think we concluded that we were in agreement, my tipsy imprecise initial explanation notwithstanding.

After a little more reflection, though, I thought it would be worth exploring this question more fully in a blog post.  In particular, I want to use the “how much does a photon weigh?” question to look at the confusion that often arises due to Einstein’s famous and mischievous equation:

,

where E represents energy, m represents mass, and c represents the speed of light.  Crudely, this equation is often referred to as defining “mass-energy equivalence.” But that description is overly simplistic and leads to all sorts of mistakes, even though — and I stress this — the equation itself is absolutely correct.

Let’s begin by describing some standard confusion that arises in talking about Einstein’s “mass-energy equivalence,” and then how to resolve it.  Beyond that, though, we will then talk about the circumstances under which we can “weigh” a photon!

The confusion in question usually starts from discussions of particles of light — photons — and the force of gravity.  In physics classes, we are taught that photons are massless particles, always traveling in vacuum at the speed of light  meters per second. In fact, Einstein’s special theory of relativity implies that being massless and traveling at the speed of light go hand in hand: anything traveling at the speed of light is massless, and nothing with mass can reach the speed of light.

So far, so good. But if we interpret energy and mass as “equivalent,” doesn’t that mean that photons have mass, too, since they have energy?  Well, no.  Einstein’s equation in fact refers to what we call the rest energy of a particle: the energy it has when it is not moving.  In a sense, this problem is resolved by our earlier statement: since a photon is always moving at the speed of light, it has no “rest energy” and has no rest mass.

A better way to put it was pointed out by Dr. Matthew Francis in his excellent 2013 post on The Meaning of Mass. He notes that Einstein himself preferred to write his famous equation in the form:

.

In other words, we should properly say “mass is a type of energy,” not “energy is a type of mass.”  You can have energy without mass, as in a photon, but not the other way around.

This isn’t the end of the confusion, however.  Everyone is taught from an early age that gravity is a force that acts between two masses; however, most people are also familiar with the prediction from Einstein’s general theory of relativity that light is also deflected by gravity¹.  One of the crucial tests of this theory was done by Sir Arthur Eddington during the May 29, 1919 solar eclipse, to see whether starlight was deflected near the sun in accordance with Einstein’s predictions.

“But wait,” the perplexed student says, “I thought that gravity was a force between masses; if particles of light are affected by gravity, doesn’t that mean that photons also have mass?”

We can answer this question, properly, by looking at what Einstein’s general relativity (GR) actually predicts.  You have probably read statements of GR more or less as follows: mass warps the fabric of space and time, making it curved.  Objects always travel by the shortest paths (geodesics), but in a curved spacetime the shortest paths are themselves curved.  What we call “gravity” is really the motion through a warped spacetime.

This is commonly depicted in images such as shown below.

But something very important about general relativity is missing from this image.  We can see clearly what that “something” is if we look directly at the Einstein field equations for gravity, namely,

.

This single expression is really a representation of 10 independent equations, and they are rather daunting even for experienced physicists at times.  We will not concern ourselves with the details of these equations², only the broad implications.  In general, the expression describes how the curvature of spacetime (left side of equation) is produced by gravitational sources (right side of equation).

But what are these gravitational sources? In Einstein’s theory, it is not mass alone that creates gravity, but energy and momentum; mass is simply a subset of energy in this theory.  The right side of the field equations, which represents the sources of gravity, is a combination of energy and momentum. Therefore, according to Einstein, energy and momentum warp spacetime, and spacetime in turn affects the motion of anything with energy and momentum.  That is, in essence, what is missing in the image above of a planet warping spacetime: some indication that all types of energy and momentum are doing the warping.

We can now resolve the confusion involving light and gravity mentioned earlier as follows.  In Newton’s theory, gravity is described as an interaction between masses; in Einstein’s theory, gravity may be described (very roughly) as an interaction between different accumulations of energy and momentum, which includes rest-mass-free photons. It could be said that Newton only recognized the largest contribution to gravitational effects — rest mass — and missed the fact that any form of energy plays a role in gravitation.

There are some surprising implications of this idea.  It has been suggested that it is possible to create a high enough concentration of electromagnetic radiation (light) to create a black hole, without any mass being used!  Such a theoretical construct is known as a “kugelblitz” (“ball lightning”).

So photons are affected by gravity not because they have mass, but because they have energy and momentum or, more accurately, because they are objects with energy and momentum moving in curved spacetime.  Our view of photons as “massless” is therefore consistent with the modern understanding of gravity, and we can breathe easier.

At last we are free to ponder the original question again: how much does a photon weigh?  It turns out to be an oddly subtle question, for a number of reasons, as we now discuss. First, we should define what we mean by “weight.”  In elementary physics, students are taught that “weight” is the force of gravity exerted on a massive object by the Earth.  Because this force of gravity is proportional to the mass of the object, we often colloquially use the terms mass and weight interchangeably, though the mass is an inherent property of an object, while the weight depends on the strength of gravity (or, in Einstein’s theory, the curvature of spacetime).  An object would weigh less on the Moon than it does on Earth, even though the mass is the same.

But things get a little weird for light.  It is affected by gravity, but has no mass.  Can we weigh it?  The simplest answer comes from asking the question: how do we weigh an object?  The obvious answer is that we take the object and put it on a scale, which measures how much downward force the object exerts.

But to do this, we need to have the object to be weighed sitting still for the measurement. Under most circumstances, a photon doesn’t sit still for such shenanigans; in this sense, we can simply say that it is meaningless to talk about the “weight” of a photon.

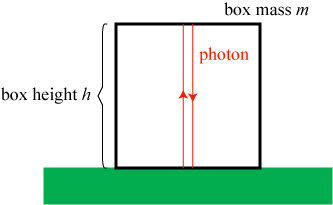
But what if we trap a photon to hold it in place? As a thought experiment, let us imagine that we trap a photon in a small box which has perfectly reflecting mirrors on its inner walls.  The photon bounces up and down forever against the top and bottom of the box, as illustrated in the sketch below.  Does the box get “heavier?”

In fact, it does!  To understand how, we need to understand a little more about how a photon is affected by a gravitational field.  You are probably aware that it takes energy and momentum for a spacecraft to escape a gravitational field; the same is true for photons moving away from a gravitational source.  As the photon climbs, it loses energy and momentum; because the energy and momentum of light are proportional to the frequency of light, the photon ends up with a lower frequency the higher it climbs.  This phenomenon is known as gravitational redshift, because the photon frequency moves toward the red end of the spectrum as it climbs.  This is illustrated reasonably well by the Wikipedia image reproduced below.

What does this mean for our photon in the box?  When the photon hits either the top or bottom of the box, it will reflect back, representing a change in photon momentum.  This change in momentum results in a net force on the box: when the photon hits the top of the box, it will produce an upward force; when it hits the bottom of the box, it will produce a downward force.

But, since the momentum of the photon is lower at the top of the box than it is at the bottom, the photon produces a net downward force on the box!  Anyone trying to pick up the box will find it requires slightly more force to pick up than it would if empty.  The box is, in effect, heavier with the photon in it.

We can actually do some crude physics calculations to estimate how much heavier the box will be!  A caveat: this is a very, very oversimplified calculation that makes many, many assumptions.  It will give us an interesting answer, however.  (If you are uninterested in the math, feel free to skip right to the punchline in italics.)

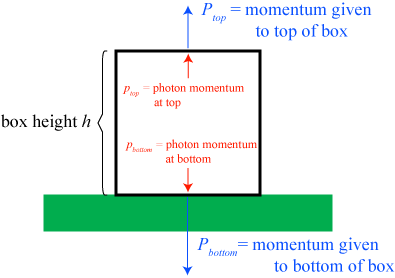
The notation we will use for this calculation is illustrated below.

Let us assume that the energy of the photon at the bottom of the box is .  From quantum mechanics, we know that the momentum of the photon at the bottom of the box is .  When the photon reflects off of the bottom of the box, its momentum reverses; by conservation of momentum, the box absorbs a momentum

.

What is the momentum of the photon at the top of the box?  Here we do some very suspect physics to get the answer!  Near the surface of the Earth, the gravitational potential energy of a massive particle is

,

where m is the mass of the particle, g is the acceleration of gravity, and h is the height of the object above the ground.  From our discussion of Einstein’s relativity, we expect that we should be able to, in general, replace the mass in this formula with the energy of an object; the gravitational potential energy of a photon is, therefore,

,

using Einstein’s to replace the mass by energy.  This potential energy is lost by the photon when it increases its height; at the top of the box, the energy of the photon is

.

This in turn implies that the momentum of the photon at the top of the box is

,

and that, when the photon hits the top of the box, the box absorbs a momentum

In one round trip, the net change in momentum of the box is

.

How often does the photon impart this momentum on the box? A round trip is a distance , and the photon travels at a speed c, which implies that it imparts this momentum over a time .

Now “force” is simply “change in momentum per unit time.” If we divide our change in momentum by the time, we get

.

The force of gravity on a massive object near the surface of the Earth is simply .  If we use from earlier, we find that the trapped photon seemingly adds an effective gravitational mass to the box directly in agreement with Einstein’s mass-energy equation!

This gives us another aspect of Einstein’s famous equation.  Evidently, when we confine energy to a small region of space, it “acts” as if it were mass, in accordance with .

This is in agreement with what we already know from nuclear physics.  In atomic nuclei, binding energies are so large that they provide a measurable change in the mass of the nucleus: in essence, a whole nucleus ends up having more or less mass than the sum of its parts.  For stable collections of protons and neutrons, the mass-energy of the whole is less than the sum of the parts, which means that energy must be added to the nucleus to break it apart. A simple example of this is deuterium, a stable isotope of hydrogen, which is a proton and a neutron combined.  The mass of a deuterium nucleus, in unified atomic mass units u, is:

.

The total mass of 1 proton and 1 neutron individually, however, is larger:

.

Unstable radioactive particles, on the other hand, have more mass than their decay products; this excess energy becomes the kinetic energy of the decay products.

Our “photon in a box” is an illustration of how trapped energy effectively contributes to the mass of an object. In this sense, we can say that a photon can be “weighed,” as long as we tightly confine it!

**********************************

¹ In fact, provided you treat light as a particle and not as a wave, one can incorporate the bending of light into Newton’s theory of gravitation.  This observation was first published by Johnann Georg von Solder in 1804, over 100 years before Einstein’s work.  The full paper can be read, translated, on Wikisource. In short: because the mass of the object being affected appears both in and in Newton’s gravitation, , one can cancel it out on both sides of the force equation and predict that light will get an acceleration a by gravity in the form

.

This calculation, though, seems a little sketchy, as it assumes that we can “divide by zero” on both sides of the force equation.  Furthermore, this Newtonian result predicts 1/2 as much deflection as Einstein’s general relativity; the eclipse experiment of 1919 was looking to see if Einstein’s numbers were correct.

² “I felt a great disturbance in the internet, as if millions of voices suddenly cried out in relief and then fell silent.”