I need to talk about more of my own research on this blog, and a new collaborative paper that just came out is a good opportunity! This paper presents collaborative work I did with researchers in India at the Physical Research Laboratory and elsewhere, building on some theoretical work I did a few years earlier. (I’ve blogged about some of the theoretical work before, so I will be dipping into that post for some of my images.)

The work in question is titled, “Simple experimental realization of optical Hilbert Hotel using scalar and vector fractional vortex beams,” and it appears in the June issue of APL Photonics. It is also a “featured” article, which means the editor found it interesting enough to feature, and is a “Scilight,” which means that the editor felt that it is interesting enough to have a separate description given!

Let’s start at the pre-history of the paper! As I’ve blogged about many times before, infinity as a mathematical concept is very weird. Though most people tend to think about infinity as unquantifiable, the mathematician George Cantor showed that one can talk about some infinities being bigger than others. In particular, the set of all real numbers on the number line (rational, irrational, transcendental) between 0 and 1 is larger than the set of all whole numbers 1, 2, 3, ..,

In the 1920s, the famed mathematician David Hilbert came up with a thought experiment to show exactly how weird infinite sets would be in the real world, an example that is now often referred to as “Hilbert’s Hotel.”

The thinking is as follows: imagine a hotel with a countably infinite set of rooms, labeled with the whole numbers 1, 2, 3, …, and further imagine that every room is occupied. The hotel then has no vacancies.

But we would like to make room for another guest, so we ask everyone to move to the next highest room: the guest in room 1 goes to room 2, the guest in room 2 goes to room 3, and so forth. Everyone can do this, since there are an infinite number of rooms. Suddenly room 1 is empty, so we have a vacancy!

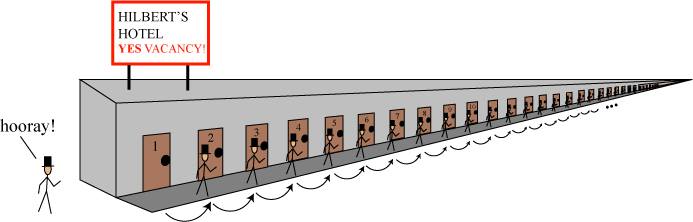
We can go further, though: we can ask every guest to move again to the next highest room, and repeat this process indefinitely, to make as many vacancies as we like! Hilbert’s Hotel therefore simultaneously has no vacancies and an infinite number of vacancies!

Hilbert introduced this thought experiment to highlight the strangeness of infinity, and arguably how it is something we should not see in any sort of real-world scenario. And yet…

We fast forward to 1974, when physicists John Nye and Michael Berry noted¹ that light waves can have structures analogous to defects in crystals, known as dislocations. These dislocations have a very regular and predictable form, in which the phase of the light wave circulates around a central point of zero intensity. If we look at the phase of typical vortex beams in a cross-section, we see examples such as follow.

The black-to-white colors represent the phase of the wave increasing by a factor of 2 pi; the number of times that the phase circulates through 2 pi is called the “topological charge” of the vortex, and it is always an integer number, and it is conserved: vortices can only be created or destroyed in pairs with equal and opposite charge.

There are many ways to make a vortex beam; one of the oldest methods is to shine a beam of light through a piece of transparent material that has a ramp-like structure, known as a spiral phase plate; if the ramp is designed with just the right height compared to the wavelength of light, it will produce a pure vortex beam.

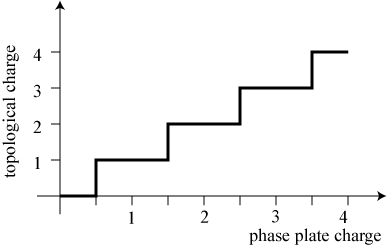
In 2004, however, Michael Berry asked^2,3 the question: what happens if the spiral phase plate is not designed to give a pure vortex? This is also the question: how can a spiral phase plate create non-zero topological charge from nothing if charge is conserved? Berry showed that the actual topological charge of the beam jumps as the effective charge of the plate passes through a half-integer value, something like as follows.

Berry also noted that just before a half-integer value, an infinite number of vortex pairs are created, starting near the center of the beam and going out to infinity, and just after a half-integer value, those vortex pairs are annihilated by each negative vortex annihilating with its opposite neighbor, leaving one extra charge in the end.

In 2015, I was working on my Singular Optics textbook, and reviewing Berry’s paper, when I realized that what Berry had described was an optics version of Hilbert’s Hotel!

I published⁴ this observation in 2016. and one of my simulations is shown below.

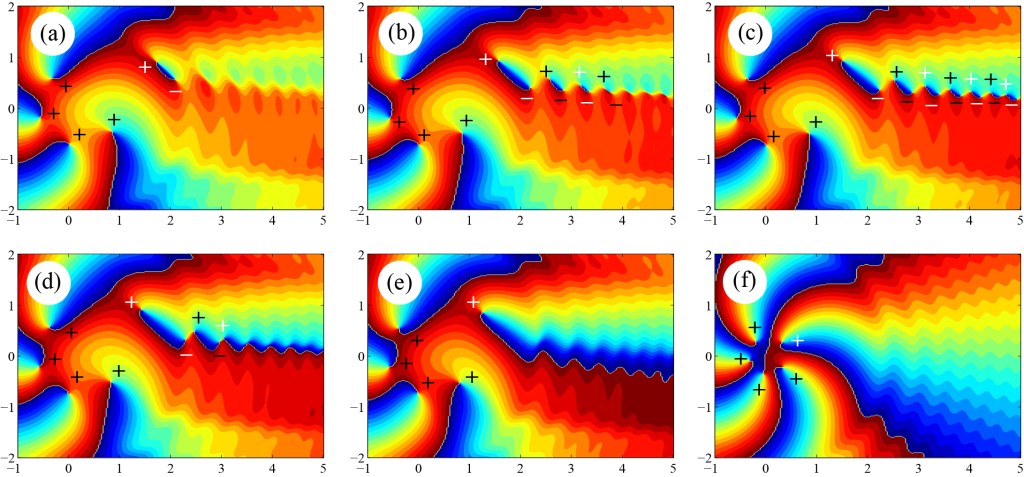
In (a) and (b), the vortex order approaches 4.5, and you can see that pairs of vortices (labeled + and -) are created; I use black and white to distinguish those pairs that are created together. When the vortex order is exactly 4.5, in (c), there are an infinite number of pairs. As the order goes above 4.5, the singularities annihilate from infinity inwards, with each negative vortex annihilating with its opposite neighbor to the right. The net result is that we are left with one extra positive vortex in (f)!

This is, incredibly, almost exactly Hilbert’s hotel. If we imagine each positive charge as a “room” and each negative charge as a “guest,” (a)-(c) represents each guest stepping out of their room. Then in (d)-(e), each guest enters the room to their right, annihilating, leaving us with one extra room (positive charge) in (f)!

I found this to be mind-boggling, and still do: we are at the very least seeing the “signature” of infinite mathematics represented in an optical system! I followed up with Berry, asking if he had noticed this analogy: he had, but hadn’t commented on it in his 2004 paper. He encouraged me to publish my observation on my own, so I did in 2016.

Another type of singularity that can appear in a light wave is a polarization singularity, where the direction of the polarization ellipse is undefined; in 2017 I published a theoretical paper⁵ showing how Hilbert’s Hotel can manifest in different ways for polarization singularities.

Flash forward to now! In 2022, one group of researchers published an experimental verification⁶ of the original Hilbert’s Hotel with the optical vortices effect. My colleagues at PRL had an idea for a different experimental configuration, however, that could also be used to test the polarization singularity case.

In simple terms: the “fractional order” of a spiral phase plate depends on the wavelength of light — if you change the wavelength, you change the fractional order. By using a tunable supercontinuum laser illuminating a fixed spiral phase plate, my colleagues were able to change the fractional order to a very fine degree, allowing a careful study of several configurations of the optical Hilbert’s Hotel. The results ended up being an almost perfect match with theory; the paper is open access, so I encourage folks to go look at the theory vs. experiment plots themselves. (I don’t want to get in trouble by publishing the figures here without permission.)

In short, our collaboration verified a number of aspects of Hilbert’s Hotel in optics that had not been seen before (such as the polarization case), and also introduced a simple and effective way to perform such Hilbert’s Hotel experiments! We are curious to see if any other aspects of infinite mathematics can manifest in optical systems, and this system allows us to consider a number of possibilities.

One final note: of course, any real optical beam is of finite diameter, so we can never “see” the infinite line of singularities, which end up being lost in the darkness of the beam edge. I like to say we can see the “signature” of the infinite case, and part of what interests me is seeing how infinity is hidden from our view in practical experiments!

*******************************************

1. J. Nye and M. Berry, “Dislocations in wave trains,” Proc. R. Soc. London, Ser. A 336, 165–190 (1974)
2. M. V. Berry, “Optical vortices evolving from helicoidal integer and fractional phase steps,” J. Opt. A: Pure Appl. Opt. 6, 259–268 (2004).
3. J. Leach, E. Yao, and M. J. Padgett, “Observation of the vortex structure of a non-integer vortex beam,” New J. Phys. 6, 71 (2004).
4. G. Gbur, “Fractional vortex Hilbert’s Hotel,” Optica 3, 222–225 (2016).
5. Y. Wang and G. Gbur, “Hilbert’s Hotel in polarization singularities,” Opt. Lett. 42, 5154–5157 (2017).
6. X. Chen, S. Wang, C. You, O. S. Magaña Loaiza, and R.-B. Jin, “Experimental implementation of the fractional-vortex Hilbert Hotel,” Phys. Rev. A 106, 033521 (2022).