![]() Right after “challenging” my fellow science bloggers to find and write about an old scientific paper, I take a hypocritical turn and write about some recent results in the theory of extraordinary optical transmission!
Right after “challenging” my fellow science bloggers to find and write about an old scientific paper, I take a hypocritical turn and write about some recent results in the theory of extraordinary optical transmission!
In a paper that came out recently in Nature*, authors Haitao Liu and Philippe Lalanne present a new model for the phenomenon now known as “extraordinary optical transmission”. The relatively simple pen-and-paper model they’ve developed provides results which are quantitatively in agreement with exact numerical simulations, and promises to be a powerful tool in the study of plasmonic nano-optical systems.
But what is extraordinary optical transmission, what are plasmons, and what is the relevance of both to nano-optics? Before I describe the results of the recent publication, I give a background on these questions, and others related to nano-optics.
Nano-optics may be loosely defined as the study of light interactions with structures much smaller than the wavelength of light. Since visible light has a wavelength on the order of 500 nanometers (0.0000005 meters), nano-optics is in essence the study of light interactions with structures between 100 nanometers to a nanometer, i.e. to a billionth of a meter.
Reasons for such studies range from the purely scientific to the almost mundanely practical, though many are related to overcoming the resolution limitations of traditional optical imaging systems. Traditional systems (such as a magnifying glass or a microscope) are only able to resolve distinct objects which are separated by a distance on the order of a wavelength or larger. This arises because a lens focuses light to a spot whose size is roughly a wavelength, and conversely the image of a point-like object will appear as a spot of wavelength size. The limit on spot size is a fundamental consequence of the wave nature of light.
However, in 1928 E.H. Synge suggested** that one could beat this limit by ‘squeezing’ light through a subwavelength-size hole in an opaque screen. The light will spread quickly due to diffraction once it emerges from the other side of the hole, but if the hole is brought very near to an object to be ‘imaged’, one can illuminate that object with a light spot whose size is no larger than the hole in the screen! This is illustrated schematically below:
Light is focused by a lens from below onto a collection of brown particles. With the lens alone, one cannot shine light on individual particles: at best, one will always illuminate three of them. If an aperture of width 1/3 of the wavelength is used to block the light, we can illuminate a single particle at a time. However, those particles must be close to the aperture, because the light field spreads rapidly upon exiting it.
There are a number of applications for this technique. In NSOM (Near-field Scanning Optical Microscopy), this probe can be used to illuminate and excite individual atoms or molecules on the surface, to study their optical properties. In nano-lithography, one uses the light field to draw subwavelength-size structures on a photo-sensitive surface. As photolithography is used to print circuit boards, the ability to write smaller structures is essential in developing the next generation of circuitry. In superresolved optical data readout, the probe is used to read/write data from an optical disk. Current compact disc technology is limited by the wavelength of light used to read/write: CDs (infrared light, wavelength 780 nm), DVDs (red light, wavelength 650 nm), and blue-ray (blue light, wavelength 450 nm). Since one can only reduce the wavelength so much (most people won’t like having a next-generation DVD player that emits X-rays!), near-field techniques provide an alternative.
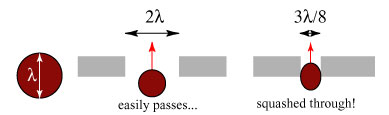
Unfortunately, all of these techniques are limited by a fundamental problem: light doesn’t easily pass through subwavelength-size holes! I often describe the situation by likening light particles (photons) to nerf balls of a diameter equal to the wavelength. One can easily pass the nerf ball through an aperture larger than the wavelength, but once the aperture is smaller than a wavelength, the ball does not readily pass through:
The classic paper about this phenomenon is by H.A. Bethe***, in which he demonstrates through idealized theoretical calculations that, for a circular hole smaller than the wavelength, the transmission is proportional to , where a is the radius of the hole and λ the wavelength. This is a terribly small number, usually less than a percent of the light actually illuminating the hole. The inability to ‘force’ light through a small hole limits the effectiveness of all the nano-optics applications described above.
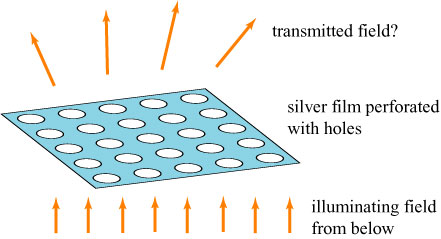
In 1998, however, a group of researchers led by Thomas Ebbesen investigated the amount of light transmitted by an array of holes, as illustrated below:
Ebbesen’s group demonstrated experimentally**** that, for an array of subwavelength-size holes in a thin film of silver, the light transmitted through the holes is much greater than Bethe predicted, at least by a factor of 10 (the original paper erroneously reported much higher gains). These results were attributed to the presence of electron-density surface waves, known as surface plasmons.
A surface plasmon is a traveling wave oscillation of electrons in the surface of certain metals with the right material properties. Because a plasmon consists of oscillating electric charges, they also have an electromagnetic field associated with them which also carries energy. A surface plasmon is illustrated schematically below:
The figure on the right is an illustration of the electric field amplitude as a function of position: the surface plasmon wave decays exponentially away from its ‘home’ surface. Among their useful characteristics: they propagate long distances along the surface of a metal without being absorbed or significantly attenuated (by ‘long’, I mean up to maybe a millimeter), they produce very high field intensities on the surface of the metal, especially near sharp edges of the surface, and they can only be converted to/from visible light by interaction with a sharp edge or a rough surface.
How do plasmons help enhance the amount of light passing through a series of holes in a metal plate? This is the point where things become a little more ambiguous. Some of the light incident upon the hole array becomes converted to surface waves, and the holes serve as a resonant cavity to boost the field intensity on both surfaces of the metal. On the transmission side of the metal, part of this high field intensity gets converted into freely propagating fields which creates a higher-than-expected transmission.
If this explanation seems a little vague to you, you’re not alone. In fact, two of the original authors of the plasmon paper later refuted their own work, insisting that the enhanced transmission can be explained using classical diffraction theory alone! The truth of the matter is that sometimes plasmons play the dominant role, sometimes diffraction theory does, but how can one distinguish the two cases? One of the major difficulties of nano-optical research, and one of the reasons it is a field of interest, is that simple models of light interacting with subwavelength structures are not readily available. To understand this better, consider the classical optics problem of the diffraction of light by a hole in a screen, and its subwavelength counterpart, illustrated below:
In the classical diffraction theory, the screen is assumed to be perfectly absorbing, the thickness of the screen is assumed to be infinitely thin, and the field in the aperture is assumed to be a “chopped-off” version of the illuminating field. In the nano-optical case, none of these approximations can be applied. When the aperture is small enough, its width becomes comparable to the thickness of the screen, and the latter cannot be neglected. Also, light is interacting with, and tunneling through, the screen as much or more than it is passing through the hole, and the screen material properties cannot be ignored. Finally, the field passing through a subwavelength aperture is highly distorted, and it is unrealistic to pretend that the field at the aperture output is equal to the illuminating field. Outside of experiment, in general the only reliable way to theoretically study subwavelength optics is to do numerical simulations. These simulations are in principle exact, but provide little insight into why various effects arise in nano-optical systems.
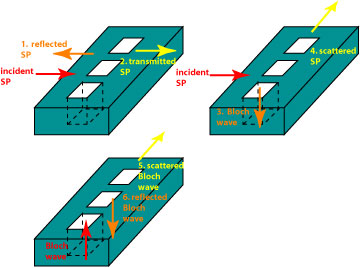
Returning to the paper by Liu and Lalanne, they partially solve this problem by deriving a closed-form analytic expression for the transmission spectrum of a hole array supporting surface plasmons. This model agrees quite well qualitatively and in some cases quantitatively with rigorous simulations using a rigorous coupled wave analysis (RCWA). Their model is based on breaking up the hole array into a collection of one-dimensional hole chains, and they define six elementary processes which can happen when light or a surface plasmon interacts with a chain, as shown below:
The six pieces represented are: 1. SP reflected by a hole chain, 2. SP transmitted by a hole chain, 3. SP converted to a Bloch wave (a wave based on the periodicity of the hole chain), and vice versa, 4. SP converted to a plane wave, 5. Bloch mode converted to a plane wave, and 6. reflection of the Bloch mode.
The unique nature of this model is that it treats the holes on what might be called a ‘microscopic’ level; instead of looking at the excited modes of the entire two-dimensional hole array, it breaks the system into individual ‘pieces’, each of which consists of a one-dimensional array of holes. In this way, the surface plasmons, the Bloch waves, and the transmitted and reflected waves are treated separately and their mutual interactions can be investigated.
I’m rather intrigued by this model; its simplicity might allow it to be used to simplify complicated optical transmission calculations. Instead of running an exact electromagnetic simulation for days, only to get a result which is difficult to interpret, one could get similar results, potentially in minutes, using this simple but apparently accurate analytic model. I’ll be giving it a much closer look in my own future nano-optical research.
*Liu, H., Lalanne, P. (2008). Microscopic theory of the extraordinary optical transmission. Nature, 452(7188), 728-731. DOI: 10.1038/nature06762
** E.H. Synge, “A suggested model for extending microscopic resolution into the ultra-microscopic region,” Phil. Mag. 6 (1928), 356.
*** H.A. Bethe, “Theory of diffraction by small holes,” Phys. Rev. 66 (1944), 163.
**** T.W. Ebbesen, H.J. Lezec, H.F. Ghaemi, T. Thio and P.A. Wolff, “Extraordinary optical transmisison through sub-wavelength hole arrays,” Nature 391 (1998), 667.





Thank you for sharing this short and sweet review of nano-optics and plasmonics research history. Working in this field myself, I believe you have done a thorough and accurate description of the important issues in the area.
hi IronMonkey,
if Skullsinthestars does not have time, would you be able to answer some conceptual questions on the topic if i sent them to you?
thanks
kavan
IronMonkey: You’re welcome! Thanks for the compliment!
Hi Skullsinthestars,
great tutorial on nano-optics!
Do you have time to answer a few clarifying questions if i sent them to you?
thanks
kavan
I’ll do my best, if you give me some time to respond!
Hello skullinthestars,
thanks a lot for the chance to ask “primitive” questions.
1) Surface plasmons are said to enhance the transmission through a 2D array of sub-wavelength apertures.
This can only be achieved with metals having a negative real permittivity. But I read that surface plasmons are a) non-radiative and b) have a k vector larger than the k-vector of photons of the same energy….
Q: How do the plasmons, being non-radiative, increase the transmittance?
Q: To generate a plasmon, does an incident photon need to have a k-vector of the same magnitude and direction? Why? Is that what resonance is? Does it come from conservation of momentum?
2) Bulk plasmons are longitudinal electron density waves in the metal. Surface plasmons travel along the interface metal-dielectric. Are they transverse waves? If so, do they oscillate in the same direction as the EM field that excites them?
3) Increase resolution: we cannot separate objects that are closer than the wavelength of the light used to image the two objects.
Why not use shorter wavelenght light and solve the problem?
You mention that if we place a sub-wavelength aperture in front of the object, very close to it, we will have better resolution. Is it because we have a stronger confinement of light in the direction of the particle before the light over-spreads? Is this improved resolution tied to a better usage of evanescent waves?
Thanks
Kavan
Hai skullsinthestars – Thanks for your descriptive explanation about nano optics and palsmons ..its very helpful to beginners in the field … and I would like to know the answers for Kavan’s questions too .. please publish a reply…
Thanks for the comment — I’ll post a reply in the next couple of days (I often take some time to think of my replies).
Pingback: FiO 2008: Day three | Skulls in the Stars
Hello sir, I am new student in this area of research and I want to know how we can calculate these six scattering coefficients which are discussed in the paper by Liu and Lalanne by using RCWA method. I am stuck in this problem please help me in solving my problem. Thank you