It is unarguably the most famous scientific equation of all time:
.
This equation, developed in the early 1900s by Albert Einstein as a consequence of his special theory of relativity, implies that energy and mass
are equivalent and interchangeable, with a constant of proportionality equal to the square of the speed of light,
. This means that energy can be converted into mass, and vice versa: this simple equation is an essential ingredient in nuclear physics, and both nuclear power and nuclear weapons (which convert mass into energy) were developed from its implications.
For another take on the equation, we can turn to Einstein himself (tip o’ the hat to Ptak):
Einstein’s remarkable success and fame has led to a lot of jealousy, and there is a small contingent of doubters — to my knowledge, all non-scientists — who seek to tear down all of his accomplishments, often by attributing them to someone else. Einstein’s most famous equation is not exempt from these criticisms; for many years some of Einstein’s critics accused Einstein of essentially plagarizing the work of German physicist Friedrich Hasenöhrl, who in 1904 suggested that a cavity containing electromagnetic (light) energy should have an inertia (effective mass) given by the formula:
.
The criticism is unfair, as Hasenöhrl made his derivation regarding a specific problem — the inertia of electromagnetic radiation in a cavity — and did not generalize it, as Einstein did, to all forms of energy (and all masses). Hasenöhrl, and others in his time, essentially failed to see the forest for the trees, and nibbled on the edge of a greater understanding. Recently, Hasenöhrl came back into the public eye due to a new analysis of his work, which treats him kindly but still gives credit to Einstein.
However, if we indulge the critics of Einstein for a moment and call Einstein’s work a ripoff of Hasenöhrl, then we must also call Hasenöhrl’s work a ripoff of the work of A.E. Dolbear! In 1881, Dolbear published a paper* with the title “On matter as a form of energy”: 23 years before Hasenöhrl!
Let’s take a look at Dolbear’s essentially unknown but fascinating speculations, and what they tell us about the significance of the work of Einstein and Hasenöhrl.
 Though Amos Emerson Dolbear (1837-1910) would not get credit for energy-mass equivalence, he managed to distinguish himself in more practical matters. He developed early versions of the telephone and the wireless telegraph, leading him to disputes of priority with the famed Alexander Graham Bell and Guglielmo Marconi. (He lost the former due to a lack of documentation, but partly won the latter.) Dolbear is also known for one of the oddest scientific laws ever: “Dolbear’s law“, introduced in 1897, which relates the chirping rate of snowy tree crickets to the temperature.
Though Amos Emerson Dolbear (1837-1910) would not get credit for energy-mass equivalence, he managed to distinguish himself in more practical matters. He developed early versions of the telephone and the wireless telegraph, leading him to disputes of priority with the famed Alexander Graham Bell and Guglielmo Marconi. (He lost the former due to a lack of documentation, but partly won the latter.) Dolbear is also known for one of the oddest scientific laws ever: “Dolbear’s law“, introduced in 1897, which relates the chirping rate of snowy tree crickets to the temperature.
Dolbear was also a well-established natural philosopher, and in his 1881 paper he turned his attention to the structure of atoms and the nature of matter in general. He begins:
In the vortex-ring theory of matter as propounded by Sir William Thomson, the characteristic differences between the elements is supposed to be due to complications in the rings themselves, as they may be knotted in innumerable ways. Several such forms are drawn in the memoir, and one such is stamped upon the cover of ” The Unseen Universe,” by Tait and Stewart.
To understand this introduction, a little background on the state of physics of the time is essential. Though the idea that all matter is composed of “atoms” goes back to the ancient Greeks, it was not until the early 1800s work of John Dalton that it became an accepted scientific hypothesis. There was, however, little experimental evidence to elucidate the nature of atoms: what exactly were atoms, and why were there different ones? Just as modern physicists today seek to unify the understanding of all of nature through string theory, physicists of the 1800s wanted to find the unifying principles of atoms.
One big breakthrough was the periodic table, developed by Dmitri Mendeleev in 1869. This table, familiar to all students of chemistry these days, arranged elements in a repeating, or “periodic”, tabular form in which elements with similar chemical properties end up in the same column. In Mendeleev’s original table, reproduced below, the similar elements were arranged in the same row. The table possessed gaps in it for which no known elements corresponded; the later discovery of those elements, with the properties that Mendeleev predicted, was a powerful confirmation of his ideas.
Mendeleev’s original 1869 printing of the periodic table. (source)
The numbers represent the relative masses of individual atoms as compared to hydrogen. An atom of lithium (Li) therefore weighs 7 times as much as hydrogen, while an atom of nitrogen (N) weighs 14 times as much as hydrogen. The striking thing in the table, quite clear to people at the time, is that the weight of almost all elements are simple integer multiples of the hydrogen weight. This was obviously an important indication of something to the researchers at the time, though nobody could say exactly what it indicated!
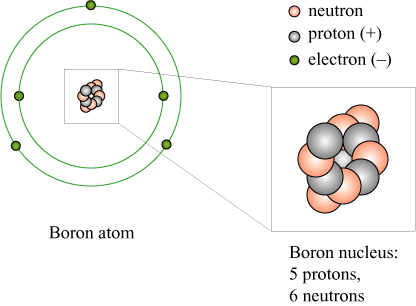
We now know that an atom consists of a (positively) electrically charged nucleus, surrounded by a cloud of (negatively) charged electrons. The nucleus itself consists of a number of positively charged protons, which dictate the chemical properties of the atom, and a number of uncharged neutrons. For example, the element boron (B) has 5 protons, 6 neutrons, and an atomic mass number of 11.
The masses of the proton and neutron are very similar to one another, and the mass of the electrons is very small in comparison. Deviations in the mass of atoms from the ideal “multiple of hydrogen” can be attributed to the neutron-proton mass difference, the electron masses, and also the mass of the binding energy of the nuclear particles, according to !
None of this internal structure of the atom was known until much later: the electron would not be discovered until 1897, the nucleus until 1910, and the neutron until 1932. In the mid-1800s, the ordered and relationships of atoms were a complete mystery.
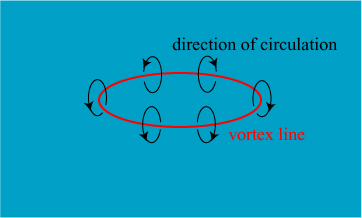
 In 1867, though, the first attempt was made** to create a unified explanation of atoms. The physicist William Thomson, eventually to take the title Lord Kelvin, became inspired by research by another distinguished physicist, Hermann von Helmholtz, on the behavior of vortices in fluids. Helmholtz demonstrated that, in perfect fluids, it is possible to create vortex “rings” in fluids that are robust and persistent. An illustration of such a vortex ring is shown below.
In 1867, though, the first attempt was made** to create a unified explanation of atoms. The physicist William Thomson, eventually to take the title Lord Kelvin, became inspired by research by another distinguished physicist, Hermann von Helmholtz, on the behavior of vortices in fluids. Helmholtz demonstrated that, in perfect fluids, it is possible to create vortex “rings” in fluids that are robust and persistent. An illustration of such a vortex ring is shown below.
Thomson got to see fluid vortices in action thanks to his colleague Peter Guthrie Tait, who demonstrated the remarkable persistence of smoke rings and their ability to bounce off of one another. The demonstrations probably looked very similar to this one on the Ellen DeGeneres show:
(It should be noted that the properties of fluid vortices are essentially the same as those of optical vortices, which I’ve discussed before.)
Kelvin saw something more than fluid dynamics in Helmholtz’s and Tait’s work: he saw a possible explanation of atoms and a unifying theory of all of physics. He envisioned atoms as vortices in a perfect fluid; these atoms were flexible, not rigid, more in line with experimental observations of matter. The differences in atoms could be explained as differences in the structure of the vortex loops, which could be knotted and linked in a variety of forms. As noted by Dolbear, one such knot is illustrated on the cover of Balfour and Tait’s The Unseen Universe:
But if atoms are a vortex in a fluid, what is the fluid? In the 1800s, physicists knew light had wavelike properties; because all waves known at the time were vibrations of some medium (water waves are oscillations of water, sound waves are oscillations of air), an invisible “aether” was hypothesized to permeate all of space. Light was therefore a wave in the aether, and Thomson speculated that atoms were then localized vortex rings in this aether! (I discuss the history of the aether in a few previous posts: see here, here, here.)
Thomson’s hypothesis gave a simple framework to interpret all physical phenomena, but it wasn’t really quantitative: that is, it couldn’t really answer many of the questions regarding atoms, such as the structure of the periodic table. Dolbear came up with an idea that could possibly change this:
This vortex-ring theory assumes that matter is a form of energy, not interchangable with the other variable forms, such as heat, electricity, etc., for the simple reason that its form renders it impossible, but if the elements be forms of energy, the law of energy may possibly be traced in them.
Here we already have the statement that is strikingly similar to Einstein’s: matter is a form of energy! Thomson’s vortex theory of atoms in essence assumes that what we think of as matter is really just a localized motion of the aetherial fluid: and that motion has energy.
Now, the energy of a given mass of matter varies as the square of its velocity, but the properties of the mass vary with the form of the energy, that is to say, the physical properties of a heated body are not identical with those of the same body when it is cool, but possesses the same amount of energy in free path motion. The physical properties of atoms and molecules vary with atomic and molecular velocities; for example, whether a piece of iron or steel is magnetic or not depends upon its temperature, that is, its rate of molecular vibration. It is not, therefore, a priori improbable that such differences as exist between the ultimate atoms constituting what we call mass, may be due to relative velocities of rotation of the vortex-ring.
The last sentence is key: Dolbear suggests that what we call “mass” is really just an artifact of the rotation of the vortex atom. But, even in that era, the expression for the kinetic energy, i.e. the energy of motion, of an object was known:
Atomic weights represent numerically these constant differences, and one might expect to find in any one of these atomic weights the two factors that constitute energy, namely a mass (or its equivalent) and a velocity; so we might write
= atomic weight. Applying this to a specific case, suppose
= atomic weight of Arsenic; by inspection it is seen that
and
. If
and
, then
= At. Wt. Carbon.
Every student of physics learns the equation for kinetic energy of a moving object in their first semester:
,
where is the mass of the object, and
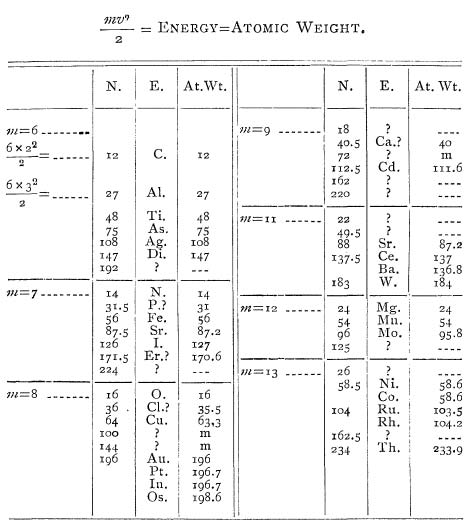
is the velocity (i.e. speed). Dolbear suggests that the atomic weight of every atom can be determined by plugging in integer values for the mass and the velocity. He demonstrates the method by constructing a table of elements:
Let a table now be constructed
and
with values 2, 3, 4, and so on, and there results a series of numbers
either exactly the same as the atomic weights of some of the elements or a very close approximation to such numbers. The elements have their symbols under
with their atomic weights as given under At. Wt. for comparison.
The table is as follows:
So Dolbear finds a striking connection between his series of energy calculations and the atomic weights of various elements. He also finds numbers that correspond to no known element — had Dolbear created a new periodic table, and discovered new elements? Dolbear himself was clearly hopeful:
By changing the value of
to 7, 8, 9, etc., a new series of numbers is obtained and the process is carried until the resulting number is higher than any known atomic weight, namely, that of Thallium 233.9. Where the number obtained is not that of any known atomic weight an interrogation point is placed. In several cases the resulting number is the same as the ones given by Mendelejeff as those of probable elements yet to be discovered; for example, in table
. 72 is such a number and is marked
in the line of atomic weights.
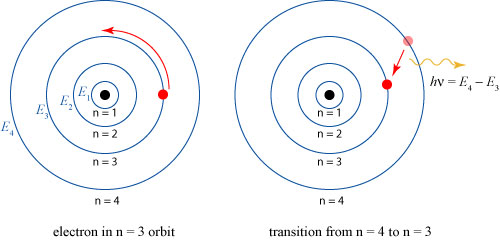
There is something else striking about this calculation, though it is not explicitly addressed by Dolbear; indeed, it can’t be! Dolbear assumes that the velocity of the vortices and the mass of the vortices are discrete quantities; this is remarkably similar to the assumption that would spark the quantum revolution! In 1913, years later than the speculations discussed here, Niels Bohr would explain the emission spectrum of atoms by assuming that electrons can only exist stably in certain quantized orbits, and emit light when they transition from a higher to a lower orbit, as illustrated below.
Dolbear seems to have introduced a quantum hypothesis of sorts in his vortex model, though he does not explicitly address this assumption. If we get imaginative, this means that this single paper contains early conceptions of both quantum mechanics and !
There is one striking problem with Dolbear’s model: if the mass of atoms is represented by , then what, exactly, is the “
” in the equation? The explanation isn’t terribly convincing:
If there be any underlying truth in this theory of calculation, then the conception of the elements will be much simplified, for it will dispense at once with complexity in the atom, and substitute a common form for all, differing arithmetically from each other in size and velocity. The only conception I have of the term
corresponding to mass, is a relative volume of ether in rotation with certain velocity.
Of course, this isn’t the only problem with Dolbear’s theory: it also happens to be wrong! Atoms are not vortices in an aether, and the aether does not exist either! Physicists, including Thomson himself, began to turn away from the vortex theory of matter in the late 1800s, and the discovery of electrons in 1897 — and their presence in the atom, which the vortex theory could not explain — pretty much ended speculation on the subject.
The “success” of Dolbear’s calculations seems to be a matter of luck and some creative accounting. Note that Dolbear matches his calculation 171.5 with erbium (Er), which has an atomic weight 170.6. — almost a whole integer off! Also, he associates his calculation 183 with tungsten (W), which has an atomic weight of 184. He makes similar stretches to make more of his number match with known elements.
Should we give Dolbear credit for being the first to explicitly discuss the connection between energy and mass? Again, we have to answer “no”. First, Dolbear explicitly states that the mass energy is “not interchangable with the other variable forms”, though the conversion of mass to energy, and vice versa, is the most significant implication of . More important, Dolbear started with a flawed premise — the vortex atom — which makes his conclusion meaningless. It is as if someone said, “2 times 2 is equal to 4 because addition is the same as multiplication, and 2 plus 2 is equal to 4.” The answer is correct, but the reasoning leading to it is wrong.
There is a lesson here about science, however. Science is not done “in a vacuum”: every major discovery is built upon other ideas, good or bad, that preceded it. As Isaac Newton famously wrote, “If I have seen a little further it is by standing on the shoulders of Giants.” Though Einstein was the one who really made the connection between energy and mass, based on the principle of relativity of motion, the idea that energy and mass are connected had been mulled over in imprecise forms years before. We need to have a more sophisticated view of “discovery”, and not credit people with scientific discovery if they are simply the first to recite a set of words or equations, and be sure to take into account the person who correctly implements the ideas.
Also, the critics of Einstein demonstrate their ignorance of history when they argue that Hasenöhrl is the true discoverer of !
**************************
* A.E. Dolbear, “On matter as a form of energy,” Science 2 (1881), 49-50.
** W. Thomson, “On vortex atoms,” Proc. Roy. Soc. Edin. 6 (1867), 94-105.




As long as we’re being fanciful, we could call Dolbear’s vortex atoms an ancestor of rotons, quasiparticles which exist in superfluid helium. The term and the idea go back to Lev Landau; Feynman figured out how to model them as tiny vortices.
Pingback: “Never Another Curie” and Other Links « Galileo's Pendulum
You don’t mention Lorentz and Poincare, who both wrote about mass-energy equivalence as a consequence of special relativity, before Einstein. Lorentz’s 1899 paper said that mass increases with velocity, and Poincare’s 1900 paper had E=mc2. These ideas were being tested in 1902, long before Einstein ever wrote anything on the subject.
Pingback: Two good blogs | OMY