Do not all charms fly
At the mere touch of cold philosophy?
There was an awful rainbow once in heaven:
We know her woof, her texture; she is given
In the dull catalogue of common things.
Philosophy will clip an Angel’s wings,
Conquer all mysteries by rule and line,
Empty the haunted air, and gnomèd mine—
Unweave a rainbow, as it erewhile made
The tender-person’d Lamia melt into a shade.

-John Keats, Lamia (1820)

Poet John Keats (1795-1821) once famously — and infamously — joked that Isaac Newton had destroyed the poetry of the rainbow by “reducing it to the prismatic colors.”  This statement has been quoted often whenever someone wants to argue that scientific knowledge dulls the beauty and poetry of nature.

Keats was being an idiot, though: a true understanding of the science behind a phenomenon  only adds to its beauty.  There are so many subtle aspects to even the simple optics of a rainbow that make it a fascinating and lovely subject of contemplation.  Once you get past the basic science of a rainbow, you are well-prepared to study more sophisticated and unusual phenomena such as this double rainbow that my wife and I saw from our house last July.

I’ve had rainbows on my mind since I was recently asked to explain some of the optics by a journalist.  Surprisingly, standard optics textbooks such as Born and Wolf’s Principles of Optics and Hecht’s Optics have no discussion of the phenomenon.  This is likely due to the fact that most optical scientists have no need to understand rainbows in their research, but this does not mean they are not objects worthy of study.

So let me endeavor to explain all about rainbows: how they form, how double rainbows form, when fully circular rainbows form, and anything else I can think of.  This isn’t just trivia: a lack of knowledge of rainbows can lead to truly humiliating consequences.

Let’s start with the short explanation: a rainbow is formed when light from the sun hits falling rain, bounces around in the raindrops and gets directed back roughly the way it came.  Each color (wavelength) of light bounces a little differently in a raindrop and gets sent back in a slightly different direction; this results in us seeing different colors from different locations, giving us the beautiful multicolored bow.

Raindrops themselves can form in a range of different sizes, from 0.5 mm in diameter to 4.5 mm in diameter.  Drops larger than this end up splitting up into smaller droplets, so 4.5 mm is in fact an upper limit.  We’re concerned primarily with drops smaller than 1 mm which are, contrary to popular perception, spherical and not tear shaped.  For sizes on the order of a millimeter, we can safely ignore the wave properties of light and treat it as a collection of rays that suffer only reflection and refraction.  The standard picture to show how a rainbow forms is then given as follows.

A ray of light from the sun coming from the left hits the droplet.  It part of the light refracts  into the water drop, gets reflected once inside, and then gets refracted out of the drop roughly back in the direction it came, at an angle of roughly 42.5° relative to the incoming ray for red light.

This picture is accurate, but can actually be a little misleading: a cursory glance at it might suggest that we see a rainbow from each raindrop.  Each ray, however, returns at a slightly different angle, and therefore is seen at a different location.  This means that each color of the rainbow comes from a different group of drops, as illustrated crudely below.

This picture also demonstrates where a rainbow forms.  The rays of the sun come from directly behind the observer and reflect off the raindrops into the observer’s eyes; this means that the rainbow is centered on the shadow of the person’s head.  Because the sun is above us when rainbows form, our shadow ends up on the ground.  The result is that we typically can only see one fraction of the rainbow, with the remainder of it effectively “obscured by the ground.”  If one is high above the ground, however, it is possible to see a complete circular rainbow, as seen for example below.

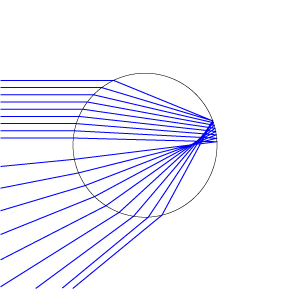
So far so good, right? Well, there’s a bit of a problem with our simple “standard rainbow explanation picture” above: it shows only one ray coming in!  In fact, each droplet should have a collection of parallel rays hitting it, each of which gets reflected back in a different direction. This is shown for blue rays below.

At first glance, it seems like we should all colors spread out over all angles, and no rainbow at all!  In fact, this is partly true: the rays shown above, and the corresponding ones for the rest of the color spectrum, are spread out and appear in the interior of the rainbow as a bright region; this can be seen in my rainbow picture at the top of the post, reproduced below.

So what distinguishes some of the rays and makes them a rainbow, where others just join into a “white noise” background?  Look carefully at the last two rays in the picture above — oh, heck, look at the same picture below with the rays drawn in red for clarity.

The two rays exiting at the lowest point in the drop — the topmost two rays entering the drop — are nearly parallel to each other, whereas all the other rays have significantly different directions.  By a curious quirk of geometry and optics, we have an entire group of rays (clustered around roughly 42.5°) that are all going in the same direction.  More rays equals more light intensity, and we therefore have an unusually bright “beam” of light leaving the droplet at those special angles.  These collection of parallel rays form the rainbow that we see.

You’ll notice that the size of the droplet plays no role in the direction that light goes on exiting; provided a droplet is spherical, it will create a rainbow in the same direction regardless of size.  This of course makes sense, because we can’t expect a rain shower to consist of a collection of raindrops of exactly the same size!

One important question has remained unanswered: what causes different colors of light to refract differently within the raindrop?  The short answer is that the speed of light in water (and, in fact, in all matter) depends on the wavelength (color) of light in a process called dispersion.  Because refraction depends on the speed of light, every color takes a slightly different path in the droplet.  Dispersion has been most famously visualized in the classic Pink Floyd album cover for Dark Side of the Moon, using Isaac Newton’s classic experiment with prisms as inspiration.

But this explanation is sort of a “punt”: we explain the rainbow by punting to “dispersion,”  but what actually causes dispersion?  The answer is fortuitously related to a recent post I did on Chladni patterns and the phenomenon of resonance.  A simple example of resonance is making a child’s swing move by pumping your legs at just the right frequency: when your motion matches the natural oscillation frequency of the swing, your movements add up over multiple swings to create one big swinging motion.  You have made the swing move by driving it at its natural, or resonant, frequency.

Atoms have their own natural frequencies associated with them that arise (very roughly speaking) from the orbit of electrons around the nucleus*.  A diagram of the Bohr atom may help here.

 

Thanks to the laws of quantum mechanics, electrons can only orbit in certain special orbits, labeled in the picture of a simple hydrogen atom above by the index n.  Each of these orbits has its own natural frequency of motion, kind of like all the planets in the solar system each have their own length of year.  When an atom is illuminated by light, the light drives the atom much like a child makes a swing move.  The response of the atom depends crucially on the relationship between the frequency of the light and the natural frequencies of the atom.  This is the origin of dispersion: this interplay between the natural oscillations of the atoms and the oscillations of the light wave that drive them.

Putting together all that we’ve learned so far, we now have a pretty substantial explanation of the rainbow!  This means we can turn to that magical and elusive phenomenon, the double rainbow.  In fact, a double rainbow is relatively easy to understand with what we’ve learned; it arises from rays of light that reflect twice inside of raindrops.

The rays from the double rainbow come back at a more extreme angle than those of the primary rainbow: by my calculation, they make an angle of about 50° with respect to the incoming ray.  This means that the double rainbow lies outside of the primary rainbow, as one can see from experience.  The colors will also be reversed, as we can see by posting the primary rainbow figure right next to the comparable double rainbow figure.

The double rainbow will be naturally dimmer than the primary rainbow.  Every time light is reflected inside the drop, part of it “leaks” out of the droplet and is lost.  The more times it bounces around inside, the more light is lost.

With that in mind, we can ask: are there higher rainbows?  In fact, it is possible on rare occasions to see the tertiary and quaternary (3rd and 4th) rainbows, caused by light bouncing around 3 and 4 times within the rain droplet, respectively!  However, these bounces cause the light to exit the drop traveling roughly in the same direction that it entered.  This means that the tertiary and quaternary rainbows can only be seen when the raindrops are between the sun and the observer.

This process can be repeated in the right laboratory conditions.  In 1998, researchers observed rainbows** up to an amazing 200th order by the use of a high-powered laser and a pendant water drop hanging from the bottom of a glass dropper of diameter roughly 2.5 mm.

So what does all of this information gain us?  As I have noted, there isn’t really a practical application for rainbow optics, to my knowledge.  However, learning about how rainbows work demonstrates that even such a simple effect has hidden complexity to it.  This complexity, in my opinion, adds another layer of beauty, giving me, I daresay, a stronger connection to the science of rainbows and to nature in general.

***

* I should point out here, lest I be accused of oversimplifying, that electrons do not actually “orbit” the nucleus.  At the atomic scale, the wave properties of electrons are dominant, and the electron can more accurately be described as a “cloud” around the nucleus.  However, this electron cloud still had natural frequencies of vibration associated with it.

** P. H. Ng, M. Y. Tse, and W. K. Lee, “Observation of high-order rainbows formed by a pendant drop,” J. Opt. Soc. Am. B 15 (1998), 2782.