Since the revolutionary development of both theories in the early twentieth century, it is fair to say that general relativity and quantum mechanics have had a rather hostile relationship to one another. One reason for this is simple a matter of scale: gravitational effects, described by general relativity, are essentially negligible in particle interactions. It is rather straightforward to calculate that the gravitational force between a pair of electrons is 39 orders of magnitude smaller than the electrical force. That is,
!
This is a very small ratio! In interactions between quantum particles, then, gravity plays no role whatsoever. Furthermore, on cosmological scales at which gravity is the dominant force, quantum mechanics has no noticeable effect.
The problem is more than just the relative size of forces, however. Quantum mechanics and general relativity just don’t seem to fit together very well, like pieces of completely different jigsaw puzzles. There are many challenges in formulating a perfectly consistent theory of quantum gravity, and we only mention one of these here. The force of gravity is determined by the distance between two massive objects, but the Heisenberg uncertainty relation of quantum mechanics states that this distance is fundamentally an uncertain quantity. An attempt to reconcile gravity and quantum mechanics is one of the fundamental driving forces behind the continually-controversial string theory.
But there have been some crude experimental glimpses at the relationship between gravity and quantum mechanics. In 1975, a collaboration between Purdue University and Ford Motor Company, of all places, researchers measured the effect of gravity on the wave properties of matter*. Though they verified quantum-mechanical predictions, their results also left some perplexing theoretical and experimental questions that are still being investigated today.
In order to understand this fascinating experiment, we first need to describe some of the fundamental discoveries of quantum mechanics upon which it is based. Quantum mechanics has a long history, but a reasonable place to mark the real “start” of the quantum theory is Einstein’s 1905 explanation of the photoelectric effect. When light of a high enough frequency illuminates a metal surface, it can eject electrons from that surface, even when the intensity of light is low. Einstein interpreted this by postulating that light, long thought to be a wave, is also in fact a stream of particles, and it is the momentum of these light quanta — now known as photons — that “kicks” electrons off of the metal.
In 1913, Niels Bohr partially solved another microscopic mystery through the use of light quanta. He showed that the mysterious light emission and absorption properties of atoms can be explained by assuming that atoms can only emit and absorb light in the same sort of discrete quanta that Einstein described. This corresponds to electrons only orbiting the atomic nucleus at discrete orbital distances.
But what causes the electrons to orbit at these special distances? This remained a mystery until 1924, when Louis de Broglie made a brilliant deductive leap. If light, long thought to be a wave, could also be a particle, then perhaps matter, long thought to consist of particles, could also be a wave? De Broglie introduced the concept of a matter wave, and it was confirmed in careful experiments in 1927. He showed, using simple calculations, that an electron wave can only fit around the nucleus at certain radial distances at which the wave makes an integer number of cycles. This model is still not completely correct, but it put to bed the notion of electrons orbiting in a classical sense: in reality, electrons are a “smeared out” wave surrounding the nucleus.

Visualization of de Broglie waves around an atom. Each more distant electron orbit has one extra “hump” in the blue electron wave.
So what are the implications of matter being wavelike? The two most important properties of waves, for our purposes, are interference and diffraction. “Interference” is the constructive addition and destructive cancellation of waves when they overlap; it is best exemplified by Young’s double slit experiment.

Young’s 1807 original drawing of the double slit experiment, showing waves emitting from the two slits combining.
Waves are emitted from two slits — labeled A and B in Young’s drawing — in the form of circular waves. When the “ups” of the two waves overlap (the light spots), the wave intensity is enhanced, and when the “downs” of the two waves overlap (the dark spots), the wave intensity is reduced. On the screen on the right, one can see that there will be dark lines at points C, D, E and F, and light lines between them.
The double slit experiment can even be done with matter, as was first achieved in 1961 by Claus Jönsson of the University of Tübingen using electrons. His image of the double slit experiment is shown below.
“Diffraction,” for our purposes, may be described as a non-geometric change of direction of a wave, particularly when it interacts with a periodic structure. You’ve likely see this all the time in your own home, if you have an LCD or LED television screen!
The rainbow streaks of light “fanning” out from the ceiling light are not part of the normal reflected image: they are the result of light being diffracted from the individual pixels in the screen. In general, one expects diffraction effects to occur when the wavelength of light is comparable to the size of the surface features the light is reflecting from.
With this in mind, we can now turn back to the 1975 “quantum gravity” experiment. Its goal was to study how the wave properties of matter are effected by a gravitational field. Classically, it is well established that objects of any mass fall with the same acceleration in the Earth’s gravitational field. Most people have are familiar with the (likely apocryphal) story of Galileo dropping two balls of different masses off of the Leaning Tower of Pisa. The two balls hit the ground at the same time, demonstrating that their mass plays no role in their motion.

The Leaning Tower of Pisa, the site of Galileo’s alleged experiment. Via Wikipedia.
When looking at the effect of gravity on the wave properties of matter, however, something strange happens. It turns out that the wave properties depend explicitly on the mass of the particle divided by Planck’s constant, known as “h-bar.” So although the classical motion of even a quantum particle is independent of the particle’s mass, the wave properties explicitly depend upon it.
By that time, experiments had already been done** to confirm that quantum particles — neutrons, in particular — fall under the influence of Earth’s gravitational field just as the classical theory predicts. In order to test the wave predictions, it would be necessary to use neutrons in an interference experiment.
You may have been wondering up to this point why it took nearly forty years for such an experiment to be attempted. On the sub-atomic scale, neutrons have a lot of mass, and in quantum mechanics this corresponds to an extremely short wavelength that gets smaller as the neutron speed increases. Even relatively slow “thermal” neutrons — moving at 2,000 meters per second — have a wavelength that is roughly 2 angstroms. This is about the size of a single atom!
For a neutron wave experiment, the implication is that the experimental device must be nearly perfect on an atomic level — even a small number of atoms out of place can wreck any interference or diffraction effects and wipe out any detectable signal. In the 1960s, however, materials scientists developed techniques to grow large blocks of silicon crystals without any crystal defects. In 1965, a set of X-ray interferometers were carved from such blocks and successfully used in experiments by Bonse and Hart***.
A photo of a Bonse-Hart interferometer is shown below. The base and the three disc-like surfaces are all carved from the same block of silicon.
So how does it work? Because the wavelength of the thermal neutrons is comparable to the atomic spacing, the neutrons “see” the atoms as a diffraction grating. Any beam of neutrons that hits a disc is split into two beams: a directly-transmitted beam and a diffracted beam, as illustrated in a top-down view below.
An incident beam of neutrons coming from the left hits disc A and is split into two identical beams, one that is the result of directly transmitted neutrons and one that is the result of diffracted neutrons. These two beams are split again at disc B, and each sends a diffracted component to disc C where they combine. The neutron waves that emerge from disc C can interfere with each other, and the counting rates measured at detectors D-2 and D-3 depends on the relative phase between the waves that traveled on the directly transmitted path and the diffracted path.
So where does gravity come into this? If the entire device is rotated around the line of the incident beam, a variable height difference can be introduced between the direct path and the diffracted path. The quantum theory predicts that this height difference will introduce a phase difference between the neutron beams at the output and, as we have said earlier, the variation of this phase difference should depend on the neutron mass divided by Planck’s constant. Their experimental results are shown in the figure below.
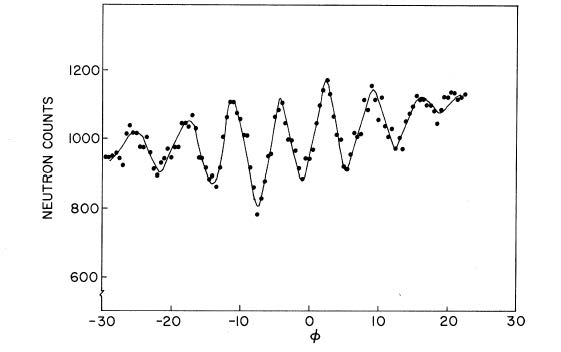
Difference in neutron count between detectors 2 and 3, as a function of the orientation angle of the interferometer. Reprinted from Colella, Overhauser and Werner, Phys. Rev. Lett. 34 (1975), 1472, with permission and copyright by the American Physical Society.
It is worth noting that this experiment ran into some unprecedented challenges. We have noted that the experiment requires the atomic structure of the interferometer to be nearly perfect; it turns out that even rotating this small device was enough to warp the structure and cause a “fake” interference effect. The experimenters compensated for this by doing the same experiment with X-rays of the same wavelength, which would not be affected by gravity in a significant manner, and determined how much of the interference pattern is due to the device warping.
So what did we learn from this experiment? The simple takeaway from it is that gravity, in its classical form at least, is compatible with basic quantum mechanics, or that quantum mechanics predicts correctly the effect of gravity on wavefunctions. The authors went a step further and argued that their results necessarily require that quantum mechanics satisfies the equivalence principle of Einstein’s general relativity. In simple terms, this principle states that a gravitational force is locally indistinguishable from the pseudo-force one experiences in an accelerated frame of reference (such as the perceived change of weight one feels when an elevator speeds up or slows down).
A deeper question, to me, is to ask what it means, exactly, that the wave properties of a particle explicitly depend on the mass through the ratio (mass)/(Planck’s constant). It may be telling us something quite profound about the nature of gravity and quantum mechanics, or nothing at all. It is, at the very least, strange to consider that a heavier particle, run through the same experimental apparatus with all other variables the same as for neutrons, would produce a different experimental result. In a mix of quantum mechanics and Earth’s gravitational field, not all masses are the same! However, as there are relatively few fundamental particles out there, we don’t really have a ready means to explore this phenomenon further.
It is to be noted that such experiments are still ongoing to this day. The original “COW experiments” (Colella, Overhauser and Werner) verified the theory satisfactorily, but more precise tests found that the theory and experiment consistently differ by a factor of about 1%. In a 2014 paper*****, it has been suggested that this discrepancy results from a neglect of the neutron’s quantum spin state.
Speaking of quantum spin, there is another neutron interference experiment that was also done in the 1970s with results that are mind-bogglingly weird… but that experiment will have to wait for another post!
Tip o’ the hat to Sakurai’s Modern Quantum Mechanics, from which I first learned about the gravity experiments discussed here.
*****************************
* A.W. Overhauser and R. Colella, “Experimental test of gravitationally induced quantum interference,” Phys. Rev. Lett. 33 (1974), 1237, and R. Colella, A.W. Overhauser and S.A. Werner, “Observation of gravitationally induced quantum interference,” Phys. Rev. Lett. 34 (1975), 1472.
** See, for instance, A.W. McReynolds, “Gravitational acceleration of neutrons,” Phys. Rev. 83 (1951), 172.
*** U. Bonse and M. Hart, “An X-ray interferometer,” Appl. Phys. Lett. 6 (1965), 155.
**** Taken from R. Colella and A.W. Overhauser, “Neutrons, Gravity and Quantum Mechanics,” American Scientist 68 (1980), 70.
***** V-O. de Haan, J. Plomp, A.A. van Well, M. Theo Rekveldt, Y.H. Hasegawa, R.M. Dalgliesh and N-J. Steinke, “Measurement of gravitation-induced quantum interference for neutrons in a spin-echo spectrometer,” Phys. Rev. A 89 (2014), 063611.







how does that quantum-ish theorem about when you zoom out from quantum to medium sized shit, QM laws become on average classical laws relate to this stuff, (if at all)?
No direct relation, as far as I can tell, between these results and the classical-quantum barrier. Since this experiment still concerns itself with, essentially, individual quantum particles in an external potential, ordinary quantum mechanics works just fine.
Really, really excellent post. Thanks for writing it!
Thank you, and you’re welcome!
Fascinating,I was impressed when Mythbusters showed that a bullet fired from a gun and dropped would hit the ground at the same time!