What a drag: Arago’s Experiment (1810)

Posted on July 5, 2008 by skullsinthestars

Note: This post is my contribution to the first-ever edition of The Giant’s Shoulders, a new blog event compiling posts concerning classic science papers.

I’ve been meaning to get back to my series of posts on relativity, but things have gone slower than I expected because of my obsessive desire to truly understand the historical scientific issues that were prevalent at the time.

In the meantime, I’ve been thinking about an interesting, infrequently-discussed topic in special relativity: the behavior of light on propagation through moving matter. This question was inspired by a comment on Uncertain Principles some time ago. In fact, one of the earliest hints of special relativity came from an experiment performed by François Arago in 1810 on ‘stellar aberration’, nearly 100 years before Einstein’s landmark 1905 paper! In this post I’ll discuss Arago’s experiment, its historical context, and the conclusions that were drawn from it.

From a historical point of view, Arago’s experiment* is absolutely fascinating: as we will see, it was a failed experiment, based on incorrect theories of light propagation, which was interpreted incorrectly by Fresnel, but this incorrect interpretation helped lead to the (correct) view that light has wavelike properties! The incorrect interpretation, however, also led physics into a hundred-year ‘red herring’ search that only ended with the advent of Einstein’s relativity. These are a lot of twists and turns to untangle, so let’s take them one step at a time.

Before 1800, most scientists were proponents of the so-called corpuscular theory of light propagation. In this view, which was championed and solidified by Isaac Newton in his 1704 book Opticks, held that light consisted of a stream of particles. Newton explicitly argued against the wave theory of light and (seemingly) refuted arguments by early wave theory proponents such as Christiaan Huygens. Newton’s arguments, and his personal gravitas, left his particle theory mostly unchallenged until the early 1800s.

There is one aspect of the particle theory of light which will be important later in the post: the explanation of refraction. When a ray of light is incident upon the flat surface of a medium, part of the ray is reflected and part of the ray is transmitted into the medium. The transmitted ray, however, is ‘bent’: it travels in a different direction than the incident ray. According to Snell’s law (experimentally determined, originally), the relationship between the angle of incidence of the ray and the angle of refraction is given by

$n_1\sin(\theta_1)=n_2\sin(\theta_2)$ ,

where $n_1$ and $n_2$ are the (experimentally determined) refractive indices of the two mediums, $\theta_1$ and $\theta_2$ are the angles which the incident and transmitted ray make with respect to the normal to the surface, and $\sin$ represents the trigonometric sine function. These symbols are illustrated below:

What happens to the speed of light when it enters a medium? According to the wave theory, refraction occurs because light slows down as it enters the medium, so that

$v = c/n$ ,

where $n$ is the refractive index of the medium, usually greater than 1, and $c$ is the speed of light in vacuum. According to Newton’s particle theory, however, refraction occurs because light speeds up as it enters the medium, so that

$v = nc$ .

(This difference is curiously similar in form to a more modern controversy: what is the momentum of a photon as it enters a medium?)

The relationship of this speed to the phenomenon of refraction differs depending on whether one applies a particle theory of light or a wave theory. Let’s look at both views, and do a little math to explain them:

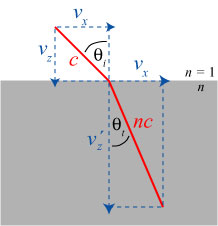
1. Newton’s corpuscular (particle) theory of light refraction. Newton argued that, upon passing the boundary between materials, the particle experienced a force in a direction perpendicular to the surface. This force results in a change of velocity in that direction, with no change of the velocity in a direction parallel to the surface. A light particle is ‘sped-up’ when it passes from a rarer medium (low index) to a denser medium (high index), and a light particle is ‘slowed down’ when it passes from a denser medium to a rarer medium. One can visualize this by picturing the surface of the medium to represent a very steep hill: a particle passing from rarer to denser rolls down the hill and gains speed at the bottom:

Let’s do a little math to see how this would work. Suppose a ‘corpuscle’ is incident from vacuum at speed $c$ with horizontal component $v_x$ and vertical component $v_z$ . This is illustrated in the figure below:

Because the total speed is $c$ , we have by simple geometry:

$\sqrt{v_x^2+v_z^2}=c$ .

We may rewrite this equation with some simple algebra to the form:

$v_z = \sqrt{c^2-v_x^2}$ .

Upon entering the medium, the new (net) speed of the corpuscle is $nc$ , the horizontal component of this is still $v_x$ , and by simple geometry the vertical component has become:

$v_z' = \sqrt{n^2c^2-v_x^2}$ .

Here is how Newton himself described the same situation (Opticks, Book one, Part I, Experiment 15):

If an Motion or moving thing whatsoever be incident with any Velocity on any broad and thin space terminated on both sides by two parallel Planes, and in its Passage through that space be urged perpendicularly towards the farther Plane by any force which at given distances from the Plane is of given Quantities; the perpendicular velocity of that Motion or Thing, at its emerging out of that space, shall be always equal to the square Root of the sum of the square of the perpendicular velocity of that Motion or Thing at its Incidence on that space; and of the square of the perpendicular velocity which that Motion or Thing would have at its Emergence, if at its Incidence its perpendicular velocity was infinitely little.

We can check that we reproduce Snell’s law by noting that

$\sin \theta_i = v_x/c$

and

$\sin \theta_t = v_x/(nc)$ .

Since $v_x$ is the same in both equations, we can solve one for the other to find that

$n \sin\theta_t = \sin\theta_i$ ,

which is simply Snell’s law.

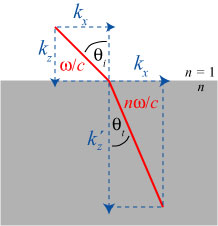
2. Wave theory of refraction. In the (correct) wave theory of refraction, the speed of light is reduced by the refractive index, so that $v= c/n$ . This in turn suggests that the wavenumber of the light, $k = \omega/v$ , where $\omega$ is the frequency of the light oscillation, is increased on entering the medium. It is assumed that the horizontal component of the wavenumber is unchanged, i.e. $k_x$ is the same both inside and outside the medium, which means that the vertical component of the wavenumber, $k_z$ , is increased. This is illustrated below:

It is to be noted that this picture is essentially the same as the Newtonian picture, with wavenumber replacing velocity! The formulas for the z-components of the wavenumber are given by

$k_z = \sqrt{\omega^2/c^2-k_x^2}$ ,

$k_z' = \sqrt{n^2\omega^2/c^2-k_x^2}$ ,

which are structurally similar to Newton’s equations for light velocity. They also produce Snell’s law, by the same geometrical arguments.

So we have two theories for the nature of light, both of which can reasonably produce Snell’s law. In Newton’s time, additional evidence leaned towards the particle theory of light, but in the early 1800s a number of experiments were performed which eventually led to the wave theory winning out**. One of the most significant was Young’s double slit experiment (discussed here and here), the results of which were reported by Thomas Young in 1807. Young demonstrated that light passing through a pair of small holes in an opaque screen will produce interference fringes on a secondary screen beyond; this interference could only be explained by a wave theory of light:

As with most revolutionary results in science, however, the full import of Young’s work would take some time to resonate with the broader community. By 1810, plenty of scientists, including Arago, were still operating under the assumption of light as a particle.

One thing that everyone agreed upon in Arago’s time, however, was the speed of light. As I’ve discussed previously, as early as the 1670s Ole Christensen Römer determined a quite good estimate of the speed of light by timing the eclipses of one of Jupiter’s moons. In short, when Jupiter is moving towards us, the eclipses seem to occur more often (the light reaches us quicker), and when Jupiter is moving away from us, the eclipses seem to occur less often (the light takes longer to reach us). From these variations, one can estimate the speed of light. Römer’s estimate was remarkably close to the modern working value of the speed of light, $c = 3 \times 10^8$ m/s.

The finite speed of light results in a number of interesting astronomical consequences, one of which is referred to as “stellar aberration”. If the Earth is moving transversely relative to a distant star, we will see the starlight arrive at an angle which depends on the speed of relative motion. If the Earth changes its direction of motion (as it does during its orbit around the Sun), we will see the starlight arrive at a different angle. In 1725, British astronomer James Bradley first observed this effect, noting that the apparent angular position of stars in the sky depends on the time of year.

This effect is actually not difficult to understand. Expanding upon an analogy from Wikipedia, suppose you are in a rainstorm, and the rain is falling directly from above. When you start to walk, you will need to tilt your umbrella slightly forward, as you are now ‘running into’ the rain. From your (moving) point of view, the rain is falling at a slight angle:

If you were to change your direction of motion (to avoid a big puddle, say), from your perspective the rain would approach from a different angle, and you would need to tilt your umbrella in a different direction.

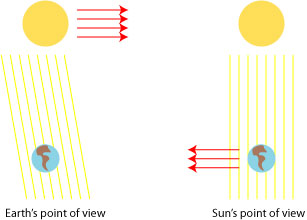
Stellar aberration is a similar effect, but with rays of light from the Sun replacing rain. Since the Earth is moving relative to the stars in the sky, it ‘runs into’ the starlight. As the Earth changes direction in its yearly orbit, the angle at which the starlight approaches changes as well. This is roughly illustrated below for the Earth and the Sun:

We can quantify the angle of the starlight in a rough mathematical sense as follows: suppose a star is directly above the Earth, and the Earth is moving horizontally below at velocity $v$ . To an observer on the Earth, the starlight does not come directly from above, but instead at an angle $\theta$ defined by

$\tan\theta = v/c$ ,

where $\tan$ represents the tangent function. In order to observe the star, the telescope must be oriented at an angle θ from the vertical.

It is to be noted that the formula above suggests that one might be able to determine the speed of light from the stellar aberration, since the velocity $v$ of the Earth is known and the angle of aberration is measurable. There was a great interest in doing so: though all measurements of the speed of light up to that point had returned the same value (within experimental error), it was assumed that variations in that speed had to exist***. Light escaping from very massive stars would have to escape a greater gravitational field, and would presumably be slowed by that field. Arago, and others of the time, assumed that light from larger stars would be traveling slower when it reached the Earth, though we know now by general relativity that this is not the case****. According to the aberration formula above, heavier stars should produce a larger aberration angle than lighter stars.

Unfortunately, telescopes of Arago’s time were not precise enough to detect this small variation in aberration angle. Arago, however, came up with a clever idea: according to Newton’s theory of refraction, the angle of refraction will be different for light particles moving at different speeds. Let’s see how this works with a little bit of math. Suppose two rays of light, one with components $v_{1z}$ and $v_{1x}$ and total speed $v_1$ , and one with components $v_{1z}'$ and $v_{1x}'$ and total speed $v_1'$ , are incident on a material surface at the same angle. Let us further suppose that the first ray is moving faster than the second, i.e. $v_1>v_1'$ . Because the angles are the same, the ratios of the components are equal, i.e.

$\frac{v_{1z}}{v_{1x}}=\frac{v_{1z}'}{v_{1x}'}$ .

What do these ratios look like for the refracted rays? Using our formula based on Newton’s theory of refraction, we have:

$\frac{v_{2z}}{v_{2x}}=\frac{\sqrt{v_{1z}^2+n_2^2c^2-n_1^2c^2}}{v_{1x}}$ ,

$\frac{v_{2z}'}{v_{2x}'}=\frac{\sqrt{v_{1z}'^2+n_2^2c^2-n_1^2c^2}}{v_{1x}'}$ .

But since $v_{1x}\neq v_{1x}'$ , we find that

$\frac{n_2^2c^2-n_1^2c^2}{v_{1x}}\neq \frac{n_2^2c^2-n_1^2c^2}{v_{1x}'}$ ,

which directly tells us that the angle of refraction depends on the speed of the incoming light particles!

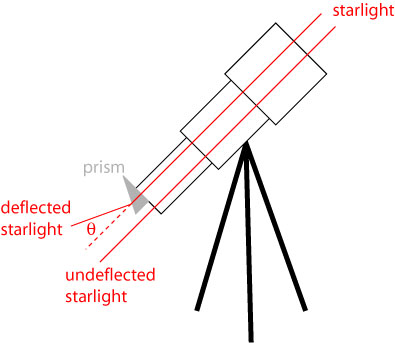
Arago’s experimental arrangement was exceedingly simple. He glued a prism to the objective lens of a telescope and looked for the deviation in the light rays on passing through the prism. The prism for his first experiments was a piece of crown-glass and a piece of flint glass fixed together, with a total angle of roughly 24 degrees. He later modified the setup so that the prism only covered half of the objective lens; in this manner he could observe the position of the star directly, as well as the position as deviated by refraction, and deduce the angle of refraction of the star. This is illustrated schematically below (note: this is a little speculative, as Arago did not include figures in his paper):

With his prism experiment, Arago could in principle directly measure the speed of light arriving from distant stars.

We need not give any more experimental detail because Arago’s experiment failed to detect any variations in the speed of light. In his own words, translated from the French,

However, by examining the preceding tables attentively, one finds that the rays of all stars are prone to the same deviations…

Light from every star is refracted the same amount! This was extremely difficult to justify using Newton’s theory of refraction, but Arago made a first faltering attempt to do so:

This result seems to be, with the first aspect, in manifest contradiction with the Newtonian theory of the refraction, since a real inequality in the speed of the rays however does not cause any inequality in the deviations which they test. It even seems that one can return of it reason only by supposing that the luminous elements emit rays with all kinds speeds, provided that it is also admitted that these rays are visible only when their speeds lie between given limits. On this assumption, indeed, the visibility of the rays will depend their relative speeds, and, as these same speeds determine the quantity of the refraction, the visible rays will be always also refracted.

In short, Arago speculated that stars radiate light over an infinite variety of speeds, and that we can only observe light whose speeds lie within a limited range of values. This was not so completely off-the-wall as one might first expect. Infrared light had been recently discovered in 1800 by William Herschel, and in 1801 Johann Ritter discovered ultraviolet light; both types of radiation are invisible to the naked eye. These discoveries are used by Arago as evidence for his supposition.

Arago’s theory is, however, wrong: the colors of light are not dictated by the speed of light, but by the frequency of light. This frequency can be changed by relative motion of source and observer, in what is known as a Doppler shift, but the speed of light is always the same, regardless of the motion of source and observer: this is in essence one of the postulates of Einstein’s relativity.

We’ll get to how Einstein’s relativity explains Arago’s results at the end of the post; before we get there, though, we take a moment to explain how researchers at the time explained them.

Newton’s particle theory of light propagation couldn’t explain Arago’s results, but the wave theory of light, at first glance, fared little better. In the wave theory of light, as understood at the time, the speed of light would be constant with respect to an all-pervasive ‘aether’. This by itself cannot be used to explain Arago’s experiment, however, because the speed of light would now depend on the relative motion of the Earth with respect to the aether: if the Earth was approaching a source of light, the speed should be increased, and if the Earth was receding from a source of light, the speed should be decreased. Such variations in speed would result in differences in the angle of refraction of light, like the Newtonian theory predicts, but in disagreement with experiment.

Another possibility is to assume that the Earth ‘drags’ the aether along with it, so that light which enters the Earth’s ‘aether field’ is not affected by the relative motion of the Earth. This fixes the problem of the refraction of light, but now predicts that stellar aberration should not occur, in disagreement with experiment!

In 1818 Augustin Jean Fresnel suggested another possibility to Arago*****: that the aether is partially dragged along with a material object. When light enters a moving medium of vector velocity ${\bf v}$ and refractive index $n$ , it has a velocity:

${\bf c'} = {\bf c}/n +f{\bf v}$ ,

where

$f = (1 - 1/n^2)$

is the so-called Fresnel drag coefficient. Fresnel’s approach represents a compromise between the ‘complete drag’ theories and ‘no drag’ theories. First, it suggests that objects with a low refractive index (for instance, the Earth’s atmosphere) produce almost no drag at all: therefore stellar aberration can occur. Second, it suggests that objects with a higher refractive index produce higher drag: this produces an agreement with Arago’s experiment.

Fresnel’s approach was convincing to Arago, who was led to abandon the particle theory of light and embrace the wave theory of light. With the confirmation by other means of the wave theory of light, Fresnel’s aether drag became an accepted part of the (incorrect) theory of the aether. In fact, an experiment was performed by Fizeau in the 1850s to explicitly measure the ‘drag coefficient’, and the results were in agreement with Fresnel’s theory.

But although Fresnel’s formula was correct, his interpretation of it was wrong. Einstein’s special theory of relativity produces Fresnel’s formula as a low-velocity special case of the relativistic velocity addition formula, as we briefly show.

*** warning: gratuitous math content! ***

In Newtonian relativity, velocities add in a straightforward way. For instance, a person on a bus moving at 50 mph who walks towards the front of the bus at 2 mph will have a speed of 52 mph relative to the street. This formula can be expressed as:

$v' = v + v_0$ ,

where $v'$ is the speed relative to the ground, $v_0$ is the speed of the bus relative to the ground, and $v$ is the speed of the man relative to the bus. In Einstein’s relativity, this velocity-addition formula takes on a more complicated form:

$v' = \frac{v + v_0}{1+v v_0/c^2}$ .

At low speeds (when $v v_0\ll c^2$ ), this formula becomes the classic Newtonian formula.

Light traveling in a moving medium is analogous to a man walking in a moving bus (light = man, medium = bus). The speed of light in the medium is $v = c/n$ , so our formula for the speed of light relative to the ground is:

$c' = \frac{c/n + v_0}{1+v_0/nc}$ .

If $v_0$ is significantly smaller than the speed of light, which it is for almost all terrestrial applications, we may make the following Taylor series approximation:

$\frac{1}{1+v_0/nc}\approx 1 - v_0/nc + (v_0/nc)^2-...$

If we substitute back into the equation for $c'$ , and keep only those terms which are linear in velocity, we arrive at:

$c' = c/n + v_0(1-1/n^2)$ ,

which is exactly the Fresnel drag formula.

*** end gratuitous math content! ***

The Fresnel drag theory helped convince scientists for six decades that the aether existed. It was only when Michelson and Morely failed in 1887 to detect any motion of the Earth with respect to this aether that the concept began to falter. Even then, it wasn’t until Einstein unveiled his special theory of relativity that scientists began to realize that the concept of an aether was unneccessary.

So Arago’s work involved many twists and turns: it was a failed experiment (no variations in the speed of light were detected), based on incorrect theories of light propagation (Newton’s corpuscular theory of light), which was interpreted incorrectly by Fresnel (aether drag), but this incorrect interpretation helped lead to the (correct) view that light has wavelike properties!

Often lost in the hubbub is the realization that Arago produced what we now know to be the first experimental evidence for the special theory of relativity, but it took one hundred years for the theory to catch up!

*********************************************

* Arago’s original paper was reprinted in his Œuvres Complètes, Tome 7, Volume 4 (1858), p. 548-568.

** Of course, when quantum mechanics arrived, light ‘regained’ at least part of its particle-like properties. We now know that light has properties of both particles and waves.

*** Though not necessarily for the reasons one might think. The Big Bang hypothesis and the idea of an expanding universe would not appear until the first half of the 20th century.

**** Gravity does have an effect on light: the frequency of light which escapes a gravitational well is shifted towards lower energies/frequencies. This is known as a gravitational redshift.

***** A translation of Fresnel’s letter to Arago can be found here.

(If you’ve read this far, I hope you’ve enjoyed the post: let me tell you, this was one of the hardest bits of research I’ve ever done. It was a drag in more ways than one!)

This entry was posted in History of science, Optics, Physics, Relativity. Bookmark the permalink.

19 Responses to What a drag: Arago’s Experiment (1810)

Yoo says:

July 5, 2008 at 11:02 am

It’s really fascinating to see how our understanding developed throughout history. Particle, wave, then both particle and wave, and all the drama that went along its development.

The way Fresnel’s approach worked almost makes it look like postulating an aether and associated drag would be a valid classical approximation to the real thing, but I have my doubts that such a model would give accurate results for anything else other than stellar aberration.

And it’s funny how the way the aether is supposed dragged brings to mind frame-dragging, and yet frame-dragging is hardly a noticeable effect in the above.

Reply
meichenl says:

July 5, 2008 at 7:33 pm

Thanks for the post! I had heard little bits and pieces of this tail (and had once worked through the “gratuitous math content”), but never knew the story about measuring the speed of light by its index of refraction. A great bit of reporting, and very clear explanations and diagrams. I’m going to be passing this link along to my relativity students.

Reply
Uncle Al says:

July 6, 2008 at 3:15 pm

There is an ANTINODE centered opposite the barrier between the pair of slits. That is the pretty thing! Also, Poisson’s Spot proves unopened cans of Coke are transparent down their long axis. Also called the Arago spot. Think of a one-zone zone plate.

Michelson and Morely were good to 10^(-8) relative. In 2007 aether was elegantly killed to at least 10^(-16) relative,

http://arXiv.org/abs/0706.2031

Two simultaneous interferometers over a year’s observation: Optical in Berlin, Germany at 52°31’N 13°20’E and microwave in Perth, Australia at 31°53’S 115°53E. An aether background could never be at rest relative to both of them. Aether optical dispersion was also killed.

Reply
skullsinthestars says:

July 6, 2008 at 7:16 pm

Yoo: It really is a great learning experience to investigate the history of early scientific discoveries. I feel I understand the ‘correct’ physics much better now that I’ve looked at the alternatives in detail.

Fresnel’s approach actually works just fine at low speeds, which is I suppose why it was accepted for such a long time.

meichenl: Thanks for the compliment! I’m glad people are finding this post worthwhile; I don’t mind saying it took a heck of a lot of work to sort it out. Psychologically, it is really hard to force yourself to learn in detail physical models which you know are incorrect.

Reply
anon says:

July 7, 2008 at 11:43 am

Even though I am a total math ninny, I enjoyed the history. Thanks for all the sweat.

Reply
skullsinthestars says:

July 7, 2008 at 4:47 pm

anon: Thanks!

Reply
stuwat says:

July 7, 2008 at 7:16 pm

Thanks for this fascinating piece of history which I had never come across before. It certainly was a convoluted path to reach our current understanding of the properties of light; I can’t wait to see where the path goes next.

Reply
skullsinthestars says:

July 8, 2008 at 2:32 pm

stuwat: You’re welcome! I’m glad you found it interesting.

“I can’t wait to see where the path goes next.”

I’m with you on that – the science and the technology are progressing so rapidly it’s hard to imagine what we’ll be able to do in a few years.

Reply
qetzal says:

July 16, 2008 at 3:21 pm

This is probably the best science blog post I have ever read! Very well written, wonderful illustrations, and a great story. Excellent job!

FYI – I’m a first time visitor, via The Giant’s Shoulders #1 on Blog Around the Clock. I see that TGS is basically your idea to begin with, so I’m doubly impressed. Somehow I missed your classic science papers challenge until now. I’m looking forward to reading those posts, as well as the rest of your blog.

Reply
skullsinthestars says:

July 16, 2008 at 6:21 pm

qetzal: Thanks for the compliment! Welcome to the blog!

Reply
Pingback: Stochastic Scribbles » Blog Archive » Light: from particle to wave
Erland Gadde says:

April 5, 2009 at 8:54 pm

Hi, a very interesting page.

I have some questions.

1. Arago found that all rays from all stars were prone to the same deviation. But what about coluor? Surely, starlight of different colours must have been deflected by different angles. Wouldn’t one interpretation of this be that corpuscles with different colous have different speeds?
What is the general view of colours in Newton’s corpuscular theory? Are the coluors connected to the speeds of the corpuscles, or to their mass?

2. Suppose that light with velocity v relative to the observer hits a prism that is stationary relative to the observer. Is it correct (as I understand it) that Newton’s corpuscular theory predicts that the prism will deflect the light at different angles measured by the observer, depending upon the observer’s and the prism velocity u relative to absolute space, since the absolute velocity c of the incoming light will be different at different values of u, although v is held constant? (v, u, and c are vectors)?
Is it also so that Arago found no such differences?

Thanks in advance and regards,

Erland Gadde

2.

Reply
- skullsinthestars says:
  
  April 9, 2009 at 2:47 pm
  
  Erland: 1. One would still see rays of different colors deflected at different angles, i.e. ordinary dispersion of light. I believe, though I’d have to check to be sure, that this would have been interpreted as the rays having different speeds once they enter the medium. I’ll also have to check about the interpretation of color in general in the corpuscular theory.
  
  2. Actually, it’s a bit more simple, as ‘absolute space’ didn’t exist in the Newtonian view: the only concern was the velocity of light relative to the observer (what you would call v). Arago expected that light arriving at different relative speeds would be deflected by different angles, but this in fact didn’t happen: as far as the prism was concerned, the speed of light was the same for light from every star.
  
  Reply
Vasant Sundar says:

August 15, 2009 at 4:07 am

It is difficult beleive that light regains speed after passing through a denser medium. By quantum theory, the lost momentum can not be regained.

We may repeat Thomus Youngs experiment with glass slab in path of one of the rays. Check if the fringes tally the location as per the calculation ( Assuming that the light regains the speed ) If they do not tally then light may not be regaining the speed.

Reply
Pingback: Levitation and diamagnetism, or: LEAVE EARNSHAW ALONE!!! | Skulls in the Stars
Rene says:

April 11, 2017 at 3:18 am

I don’t understand why Arago was convinced that the velocity of the star light has an effect on the refraction angle in the prism.

As far as I can tell Snell’s law had not been proven at that time. Also, Newton’s explanation of the refraction was just that: an explanation.

Couldn’t Arago just have assumed that Snell’s law and Newton’s explanation are “obviously” wrong, and that for an (unknown) reason the angle in the prism is constant?

Reply
hiroji kurihara says:

October 21, 2018 at 8:07 pm

Numerical values of a few sorts of aberration will show that propagation of light follows aether frame and air frame.

So, in the two, Doppler effect of light will be the same as that of sound. The formula is the same also.

http://www.geocities.co.jp/Technopolis/2561/eng.html
My web-site above disappear on 31 Mar 2019 (because of the end of Yahoo’s service).

Sorry, I cannnot receive E-mail. I do not have PC.

Reply
michael sotiriadis says:

December 1, 2020 at 2:31 pm

Very nice! But wait a minute. How did Fresnel find the value of his coefficient = 1-1/n2 ?

Reply
Dek says:

February 27, 2024 at 3:19 pm

What is a wave?

Is it a thing in its own right? Explain.

Or is its quality a result of a force working within a medium?

Definition please.

Reply