The best stories in the history of physics are those in which someone comes from humble origins and, seemingly out of nowhere, makes a brilliant discovery that changes everything.  Such stories, however, can give a very misleading impression of the nature of scientific progress: science is a continuous process, and a closer inspection of any incredible breakthrough always reveals that there were numerous earlier discoveries that anticipated it.

A great case study of this is Einstein’s special theory of relativity, introduced in 1905.  Einstein’s groundbreaking work transformed mankind’s perceptions of space and time, provided answers to puzzling problems and led directly to other major discoveries, including the harnessing of nuclear energy.  However, Einstein’s revelations were preceded by some twenty years of gradual progress, during which time researchers put forth tantalizing hypotheses that came closer and closer to the truth.

One such discovery was made in 1889 by George FitzGerald.  To explain a seemingly incomprehensible experimental result, he suggested that objects in motion shrink along their direction of travel.  In this post, we will discuss what is now known as the FitzGerald-Lorentz length contraction and explain how FitzGerald fell short of the astonishing ideas that would be conceived by Einstein.

The history behind the confusion and FitzGerald’s solution stretches all the way back to the beginning of the 19th century.  Since the publication of Newton’s Opticks in 1704, scientists had been convinced that light consisted of a stream of particles, referred to as corpuscles.  In the early 1800s, however, Thomas Young demonstrated that light possesses wavelike properties with his famous double-slit experiment, and within the next decade most researchers had come around to idea that light is a wave.

This wave nature of light introduced its own problems, however.  All waves known at that time were vibrations of some sort of material medium — water waves are oscillations of water, sound waves are oscillations of air, and waves on a string are oscillations of the string.  What were light waves oscillations of?  A hypothetical substance known as the “aether” was introduced: invisible, non-tangible and only detectable through the light waves excited in it.  This aether model seemed to explain a number of curious observations regarding the propagation of light, and by the late 1800s it was an unchallenged part of physics.

The supposed existence of the aether became more and more vexing as time went on, however.  If there was this material, permeating all space and all matter, it should be detectable somehow, right?  Some scientists attempted to deduce the properties of the aether through theoretical reasoning, but these attempts also felt unsatisfying.

The best strategy that arose for at least indirectly observing the aether was to measure changes in the speed of light due to the motion of the Earth.  The speed of light was presumably constant with respect to the fixed aether, but an observer moving in the aether could potentially see a faster and slower speed.  The effect would be similar to measuring car speeds while driving down the freeway: cars driving in the same direction are moving relatively slower, while cars driving in the opposite direction are moving relatively faster.  Similarly, light moving parallel or anti-parallel to the Earth’s motion would, according to the aether theory, be measured as moving slower or faster than expected, respectively.

The Earth was already known to move at 30 kilometers/second in its path around the Sun. It would have to be moving, at some point in its orbit, at least at this speed relative to the aether. Even though nobody knew how to directly measure the aether, one could presumably indirectly detect it by measuring changes in the speed of light as the Earth moves.  These changes would be very small, however, considering the speed of light is 3,000,000 kilometers/second, and would require a very sensitive measurement apparatus.

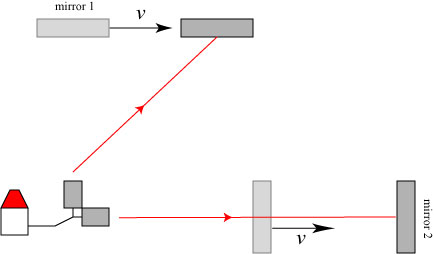
Such a device was built and employed by Albert Michelson and Edward Morley in 1887, in what would quickly become known simply as the Michelson-Morley experiment.  The experiment uses the interference of light waves to measure changes in the speed of light, and the setup is illustrated below:

A light beam is incident from the left. It hits a half-silvered mirror which is inclined at a 45 degree angle, which splits the beam into two parts: one which is reflected, one of which is transmitted. Each fraction of the beam travels to a mirror and back, and at the half-silvered mirror they are recombined and their sum is projected onto a screen. When the light recombines from each arm of the interferometer, we get an interference pattern on the screen.

To understand how this allows us to measure the motion of the Earth in the hypothetical aether, we consider a simple analogy of boats in a river.*  In this case, the boats represent the light traveling through the two arms of the interferometer, and the flowing river represents the aether moving relative to the experiment:

Each boat has a top speed of c, and the river flows to the right with velocity v. Boat 1 travels a distance d from point A to point B, and then returns, while boat 2 travels a distance d from point A to point C, and then returns. How long does it take each boat to return to the starting point?  Boat 2 moves very fast with the current on the way to C, but moves very slow against it on the way back.  Boat 1 must steer partly upstream in order to cancel the motion of the river, and its speed across the river is somewhat reduced:

The detailed mathematics is presented at the end of this post, but the net result is that boat 2 actually takes a longer time to make its round trip than boat 1.  This difference can be measured using the interference of light waves.

The problem, as it seemed to be at the time, is that Michelson and Morley could detect no difference in travel times between boats… ahem… light beams!   According to their experiment, the speed of light seemed to have a fixed value, independent of the relative motion of the Earth with respect to the aether.  As you might imagine, this presented a problem for the already somewhat ailing aether theory, and researchers scrambled to explain what was going on.

The first good guess came from George FitzGerald (1851-1901), an Irish professor of natural science at Trinity College, Dublin.  In 1889, he published a short paper in Science titled “The Ether and the Earth’s Atmosphere” which came up with a very straightforward explanation of the Michelson-Morley experiment: he suggested that the experimental apparatus might be shrinking in the direction of motion!

The full text of FitzGerald’s letter**, which is very short, is reproduced below:

I have read with much interest Messrs. Michelson and Morley’s wonderfully delicate experiment attempting to decide the important question as to how far the ether is carried along by the earth.  Their result seems opposed to other experiments showing that the ether in the air can be carried along only to an inappreciable extent.  I would suggest that almost the only hypothesis that can reconcile this opposition is that the length of material bodies changes, according as they are moving through the ether or across it, by an amount depending on the square of the ratio of their velocity to that of light.  We know that electric forces are affected by the motion of the electrified bodies relative to the ether, and it seems a not improbable supposition that the molecular forces are affected by the motion , and that the size of a body alters consequently.  It would be very important if secular experiments on electrical attraction between permanently electrified bodies, such as in a very delicate quadrant electrometer, were instituted in some of the equatorial parts of the earth to observe whether there is any diurnal and annual variation of attraction, — diurnal due to the rotation of the earth being added and subtracted from its orbital velocity; and annual similarly for its orbital velocity and the motion of the solar system.

We can illustrate FitzGerald’s idea quite readily.  Boat 2 takes longer than boat 1 to make its round-trip; suppose, however, that the force of the moving water scrunches up the shoreline, making the distance between A and C shorter:

So the marker buoy at C ends up getting pushed to the point C’, and boat 2 has to move a shorter distance d’ instead of distance d.  If d’ is just the right value, the two boats will take the same amount of time to perform their round trips.

This is the idea behind FitzGerald’s length contraction.  Since the aether was (in 1800s physics) the medium that communicated electromagnetic waves, and atoms and molecules are held together by electricity, it was reasonable to assume that moving through the aether might apply an electric pressure of sorts, causing an object to shrink along the direction it is moving.  A full-size car, driving fast enough through the aether, would shrink to a compact!

Obviously this shrinkage would be generally very small, only becoming appreciable when one’s speed with respect to the aether approaches the speed of light.

FitzGerald even suggests a way to test his hypothesis.  If electrical forces depend on one’s motion through the aether, it should be possible to see daily (diurnal) variations due to the Earth’s rotation: during half of the day, the Earth’s rotational motion will add to its orbital motion, and during the other half of day, it will subtract.  Also, on a yearly basis, during half of the year the Earth’s orbital motion will add to the motion of the solar system through the aether, and during the other half of the year it will subtract.

Nobody seems to have taken up FitzGerald’s experimental suggestions, though Lord Rayleigh attempted to demonstrate this shrinkage using another clever optical technique — and failed.  In 1895, Hendrik Antoon Lorentz developed the idea of length contraction even further, developing a detailed set of equations that describe the properties of an aether that shows no change in the speed of light; the idea of length contraction is therefore known today as FitzGerald-Lorentz length contraction.  Lorentz, at least at first, viewed length contraction as an inevitable consequence of Michelson and Morley’s work (translation from Larmor’s Aether and Matter, 1900):

However extraordinary this hypothesis may appear at first sight, it must be admitted that it is by no means gratuitous, if we assume that the intermolecular forces act through the mediation of the aether in a manner similar to that which we know to be the case in regard to electric and magnetic forces.  If that is so, the translation of the matter will most likely alter the action between two molecules or atoms in a manner similar to that in which it alters the attraction or repulsion between electrically charged particles.  As then the form and the dimensions of a solid body are determined in the last resort by the intensity of the molecular forces, an alteration of the dimensions cannot well be left out of consideration.

The solution to the mystery was provided at last by Albert Einstein in 1905, in an amazing and genuinely paradigm-shifting paper.  Whereas FitzGerald and others focused on the aether as an “absolute” property of nature around which to construct the laws of nature, Einstein instead declared that the speed of light is the “absolute”: every observer, regardless of what their state of (constant) motion, measures exactly the same speed of light.  Einstein coupled this postulate with the postulate of relativity: the laws of physics are the same for every observer moving at constant velocity.

Einstein’s interpretation of the Michelson-Morley experiment is quite simple: since the speed of light is the same for every observer, the light traveling in each arm of the interferometer is simply traveling at the same speed, meters/second.  No motion of the Earth will change these values.  The laws of physics for an observer moving at a constant velocity are the same as those for an observer standing still.  This also results in the observation that there is no such thing as “standing still”, in an absolute sense — there is no experiment that can be done to measure one’s “absolute motion”.

As a side effect, Einstein’s theory actually includes a form of length contraction, but of a fundamentally different nature than FitzGerald’s.  Let us imagine a modified version of the Michelson interferometer, which fires simultaneously two ultrashort pulses each of which propagates a distance  to a mirror and returns to a detector at the point of origin. If both pulses arrive at the same time, a siren goes off to unambiguously announce their simultaneous arrival. From the point of view of the laboratory, each pulse travels the same distance at the speed of light  and returns, firing off the siren.

Now let us consider this from the point of view of an observer who sees the experiment moving past him at a velocity :

The new observer sees the light heading towards mirror 1 on a diagonal trajectory, and the light heading towards mirror 2 must chase the moving mirror, taking longer to reach it.  According to Einstein’s relativity, however, and distinct from the aether/boat case discussed earlier, the new observer measures the velocity of light to be  for the light moving along both paths!

Because the siren goes off, we know that the light pulses arrive back at the detector at the same time.  As we have seen from the boat example, if the distances to the two mirrors are equal, it should in fact take a longer time for the light to return from mirror 2.  The only conclusion that the second observer can draw is that the distance between the source and mirror 2 has contracted, i.e. length contraction has occurred!

Herein lies the difference between the FitzGerald form of length contraction and the Einstein form.  In the FitzGerald version, both the first and second observer can agree that the experiment is moving.  The observer moving with the experiment would in principle be able to measure a change in the electrical forces between molecules, demonstrating a motion in the aether.  In the Einstein version, the two observers agree that the speed of light is c, but disagree on the distances that the light has to travel.  The ideas of absolute motion and absolute distance for every observer have been replaced by the idea that the laws of physics are absolute for every observer, and the details such as space (and time) are arguable!

Einstein’s theory represented a huge change in mankind’s perception of nature and the universe.  Space and time were relegated from absolute quantities to relative ones depending on an observer’s state of relative motion.  Nevertheless, others were already anticipating Einstein’s discovery before him.  Lorentz, who was a proponent of the FitzGerald contraction hypothesis, also derived a mathematical transformation between observers — the Lorentz transformation — that left the speed of light constant for all observers.  This transformation is now a part of Einstein’s relativity.  Other scientists such as Ernst Mach and Henri Poincaré had already in the late 1800s begun to dismiss the notion of absolute space and time, and the aether along with it, and propose a new theory of relativity.  In fact, one distinguished scientist stubbornly refused to accept any real significance in Einstein’s relativity work.

Einstein, however, was the one to bring all the scattered musings of the different scientists together into a new principle of physics.  Where the others were inching towards a new theory of relativity, Einstein leapt towards it wholeheartedly.  It was a great discovery, but the earlier efforts of others such as FitzGerald show that Einstein’s work was part of a greater effort to understand the nature of space and time.

***************************************

* I’ve adopted the boat discussion from an earlier post on measuring the speed of light, with some updates.

** G. FitzGerald, “The Ether and the Earth’s Atmosphere,” Science 13 (1889), 390.

***************************************

The math of the time-delayed boat problem:

Each boat has a top speed of c, and the river flows to the right with velocity v. Boat 1 travels a distance d from point A to point B, and then returns, while boat 2 travels a distance d from point A to point C, and then returns. How long does it take each boat to return to the starting point? We can use a little geometry and velocity addition to determine this. Boat 2 will have a total velocity of c + v on the way out to point C, and will have a total velocity c – v on the way back. Boat 1′s velocity is slightly more difficult to calculate; in order to travel straight across the river, it must have a velocity v against the river flow, and a total velocity of c. Using some simple geometry,

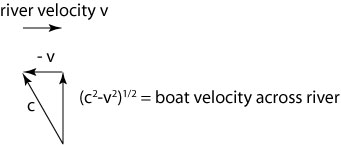
Boat 1 must have a speed moving from A to B, and an identical speed for the return trip. Since the amount of time it takes for a trip is the distance divided by the speed, we therefore find that the transit times for the boats are as follows:

,

.

The net result is that boat 2 takes a longer time to make its round trip than boat 1.

FitzGerald’s length contraction “fixes” the time discrepancy if the distance from A to C is shrunk to a value

.

**************************
G. FitzGerald (1889). The Ether and the Earth’s Atmosphere. Science (New York, N.Y.), 13 (328) PMID: 17819387