In part II of my series on ‘What is a wave?’, I addressed one of the two most significant behaviors of waves, namely interference, the ability of a wave to ‘interact’ with itself. The second behavior of waves which is extremely significant is diffraction, and we will address it in this post.
Diffraction may be broadly defined as the tendency of a wave traveling in two or more dimensions to spread out as it propagates. The most significant consequence of this spreading is the ability of waves to ‘bend around corners’ when faced with an obstacle. We all have experienced the diffraction of sound waves: if you and a friend stand on opposite sides of a large building (say a farmhouse) in the middle of an open field, you will be able to talk to each other even though there is no direct ‘line of sight’ between you and your friend, and no ability for the sound waves to reflect off of intermediate surfaces. The sound waves wrap around (diffract around) the outside of the farmhouse, allowing communication.
Light waves also diffract, though the effect is much smaller and difficult to detect. This is because the wavelength of visible light (to be discussed in part IV of optics basics) is much smaller than the wavelength of sound. One can demonstrate theoretically that waves only produce appreciable diffraction when interacting with objects of a size comparable to or smaller than the wavelength. Wavelengths of sound can range between millimeters and meters (comparable to a farmhouse) while wavelengths of visible light are on the order of 500 nanometers (0.0000005 meters, or 0.5 micrometers).
To give you an example of how a diffracted field would differ from a field propagated geometrically, we consider the case of light traveling through a narrow slit in a metal plate:
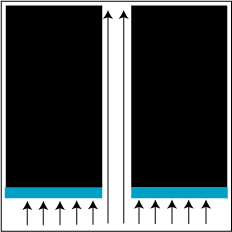

In both pictures, higher light intensity is represented by brighter color. In both pictures, we have a collimated (one-directional) field incident from below upon an aperture in a silver plate (represented in cyan here). The wavelength is taken to be 500 nm, the aperture width is 500 nm (i.e. one wavelength), and overall the images are 4000 nm by 4000 nm.
The first picture indicates the prediction of geometrical optics. Geometric theory models light as traveling along definite paths (rays) in space, indicated on the picture by arrowed lines. Those rays which hit the metal plate are absorbed or reflected, while the rays illuminating the aperture pass directly through unimpeded and form a ‘column’ of light.
The second picture is an exact numerical simulation of Maxwell’s equations, demonstrating what ‘actually’ happens when light illuminates a wavelength-wide slit. Two things are different from the geometric picture: below the aperture, there are horizontal lines of darkness along with the bright lines. These are locations where the incident field from below is interfering with the field which gets reflected from the metal plate. More important for our discussion, however, is what happens when light passes through the aperture: not only are there bright and dark patches indicative of interference, but we can see that the light is spreading in a cone away from the aperture, at odds with the simple geometric prediction. Some of the light has evidently ‘bent around the corner’ on passing through the aperture, and this is what we mean by diffraction.
We’ve mentioned above that diffraction is only appreciable when light interacts with objects of size comparable to the wavelength, and this is true of light passing through the slit, as well. The figure below shows an exact simulation of light passing through an aperture which is 3 wavelengths wide:

This picture can be compared with the geometric one shown previously. Although interference and diffraction effects can still be seen, they are much less prominent in this case, and to a good approximation light is propagating in a narrow ‘column’ of width equal to the aperture. Diffraction effects are still present even at larger aperture sizes, but they become insignificant compared to the overall geometric behavior.
The mathematical theory of diffraction is relatively complicated, and requires a significant amount of vector calculus, so we won’t go into too much detail here. We can understand it a little better, however, by the use of the Huygens construction. Christiaan Huygens (pronounced ‘hoy-gens’ in English, but closer to ‘how-gens’ in Dutch) was a Dutch mathematician/scientist who lived from 1629-1695. He developed the first wave theory of light, and described the propagation of light by means of the Huygens construction: treat every point of a wavefront as the source of a new spherical wave. The position of the new wavefront is constructed by tracing the boundary of all these ‘secondary’ wavelets.
This is illustrated below. The top image shows the construction for an infinite plane wave which is uniformly traveling upward. The construction shows that the wavefronts remain planar. The bottom image illustrates aperture diffraction in Huygens construction; because the wavefront is ‘clipped’ at the edges of the aperture, the wavelets on the edges spread out into the ‘shadow’ region of the aperture:

Borrowing from one of my thesis advisor’s talks, here’s a picture that Huygens himself drew in his manuscript on the subject, showing the secondary wavelets of a candle flame:

Huygens’ work was not enough, however, to conclusively illustrate the wave nature of light. Only when Thomas Young introduced the principle of light interference in 1801 was the theory complete enough to match experiments and make convincing theoretical predictions. That history, however, will have to wait for another post!
Diffraction effects are hugely important in optical science and engineering, and we’ll be addressing the applications and consequences of diffraction as my blog continues. In my last post on optics basics, I’ll introduce some of the basic quantities used to describe waves, such as wavelength and frequency.


I’d like you to address bodysurfing at some point. Without the human family having fun on the beach, everything’s moot. Remember that when Fitzgerald published “Tender is the Night,” a Marxist critic said, “Dear Mr. Fitzgerald: you can’t hide from a monsoon under a beach umbrella.” Well I think you can. And I think you might agree with me. I dig the technical stuff too, though, straight up.
All of the optics is bang-on, but I think you are over-stretching the analogy to sound waves a bit. The sound-wave bending you mentioned occurs because sound waves propagate by jostling molecules, with each molecule acting like a Huygen’s point source. This causes rapid diffusion in all directions, including backwards. For example if two people stand back-to-back in an open field with no large objects to reflect or diffract the sound waves, they can still hold a conversation. I’m not sure that can be called “diffraction.” What do you think?
PD wrote: “All of the optics is bang-on, but I think you are over-stretching the analogy to sound waves a bit.”
What??!! You doubt me??!! You are so gonna get banned!!! 🙂
Seriously, though, I think my analogy works just fine. Mathematically, the air pressure satisfies an ordinary wave equation, provided one is dealing with relatively small pressure changes (to avoid nonlinear effects). This is similar to the reality that vibrations on a string satisfy a wave equation as long as the vibrations aren’t too large. Within these limits, the diffraction theory of sound is mathematically identical to the scalar theory of light diffraction. (I broke out my copy of Theoretical Acoustics, by Morse and Ingard, to make sure of this.)
Concerning your example, I suspect you’re confusing primary sources with secondary sources, which is a common slip-up in optics. Primary sources are the generators of the wave, while secondary sources are modifications of already generated waves (such as passing a wave through an aperture). Mathematically, a primary source and a secondary source have different Green’s functions representing them – primary sources are spherical waves, while secondary sources are the Huygens wavelets. A person screaming something is essentially a primary source, with some imperfect directionality created by their mouth and body, I would say.
These complications are exactly why I chose my example of ‘farmhouse diffraction’ very carefully, with no regard as to the generator of the sound. My only concern was that the source and receiver did not have direct line of sight, which means the only way that sound could get from one to the other is by waves bending around corners.
Perhaps my objection is more clear if we reverse the analogy. When light passes through an aperture, the aperture causes the light to “bend”. It is the obstacle that causes the new behavior. In your acoustic case of two people around a corner, would you similarly say that the existence of the barn is what is causing the two people to be able to hear one another? The answer is “no.” They would have heard each other anyway. Because that is the case, then the reason they can hear each other is not diffraction.
You can, of course set up an acoustic scenario that demonstrates diffraction, but you would probably want to use a more controlled acoustic source, like a parabolic speaker, to create a more directional sound wave. I think a better example of diffraction in every day life would be ripples on the surface of the water (basically a 2D version of the string cases you have used throughout this tutorial). If a ripple hits a wall with a small opening, you see exactly the diffraction effects you are discussing.
PD wrote: “In your acoustic case of two people around a corner, would you similarly say that the existence of the barn is what is causing the two people to be able to hear one another? The answer is “no.” They would have heard each other anyway. Because that is the case, then the reason they can hear each other is not diffraction.”
Hmm. I’m not sure what you mean. How would they have heard each other anyway? I think you’re making things too complicated. I consider diffraction to be effects associated with non-rectilinear propagation, e.g. light bending around corners. Non-line-of-sight propagation in a homogeneous medium is always diffraction, to the best of my knowledge.
The example I give isn’t really any different than examples in optics. Edge diffraction (light bending around an edge of a ‘black screen’, or corner) is well known and understood. The so-called Poisson or Arago spot, in which a bright spot appears in the center of the geometrical shadow when illuminating an opaque disk, was the experiment which really confirmed the wave theory of light for people.
You’ll have to clarify what you mean by ‘heard each other anyway.’ I chose the ‘big barn in a field’ example to avoid two specific complications: 1. penetration of the wave directly through the barn, and 2. reflection of the wave off of other objects.
skullsinthestars wrote: “I consider diffraction to be effects associated with non-rectilinear propagation, e.g. light bending around corners. Non-line-of-sight propagation in a homogeneous medium is always diffraction, to the best of my knowledge.”
Ah… this is exactly either my point, or the point of my confusion.
The reason I think “the barn” example is confusing is that most people’s experience with sound is that it does not travel in straight lines. Air acts like a scattering medium, and I am not sure you would call such scattering a diffraction effect.
I had a dream. In my dream I had built a giant disk, and there were a bunch of slots around the outside edge. I had a motor that spun the disk very fast. I shined a laser through the slots, which were each 1 lightwave wide, and the metal between the slots was also 1 lightwave wide. The disk spun so fast that each slot was open for 1 cycle of the light and then closed for one cycle. I woke up wondering what it meant.
For the last half hour or so I’ve been thinking about it.
The light from the left half of the slit overlaps the light from the right half, but to each side one of them is delayed. Straight ahead you get one cycle of light and then a cycle of darkness, repeated. That would turn into some harmonic series.
Off to the side enough that normally you’d get a dark gap because the right side comes in half a cycle behind, now you get a crest, and a half-cycle of darkness, and then a trough and a half-cycle of darkness, repeated. I imagine that would turn into a different harmonic series.
Where you would normally get your first constructive interference band, you would reconstitute the original wave.
So at each place you’d normally get destructive interference you’d get half cycles separated by blanks, and at the places you’d normally get contructive interference you’d alternately get reinforced cycles separated by blanks, versus the original wave.
But then I thought, what if you tried this with water waves? Water waves maintain themselves by pressure and height differences in a medium. If you cut out every second cycle, a water wave would quickly reform itself into just a wave with half the frequency and double the wavelength. Wouldn’t it?
What would actually happen? Do light waves move independent of what’s around them, or does each section of the wave depend on the rest of the wave to maintain its integrity, like water waves? Or is this an example where they behave like particles instead?
I tried to imagine actually doing the experiment. With a 1 hertz radio wave my slits would have to be 186,000 miles wide. Not very practical. Make the wavelength smaller. The outside edge of the disk has to move at 1 wavelength/cycle, Is that lightspeed? Maybe there’s some other way to do it.
Now that I’m awake, here’s the idea I’d like to find a way to explore. Water waves retain the shape their medium demands. Pressure waves in an incompressible liquid turn into vertical height, and the high water goes downhill, and it turns into a minimum-energy shape. Does light behave like that? Or does the source of the light make electric and magnetic fields that then propagate independent of each other and independent of their own preceding and following components?
I guess the question kind of answers itself. To the extent that Maxwell’s equations fit reality, electric and magnetic waves can’t have a sudden cutoff like I described. Do they immediately form a shape that fits ME if they get distorted away from that shape? Or is matter that emits EM radiation forbidden to move in ways that would generate a different shape? There may be no way to tell between those. If I can’t move matter in ways that would make perverse waves — if my beam-splitter and everything like it is impossible, then I’m left with an unsatisfying argument about some alternate reality.
It was a nice dream.
Not sure about your dream, but the spinning wheel sounds a lot like Fizeau’s experiment, which originally was developed to measure the speed of light!
Pingback: Rolling out the (optical) carpet: the Talbot effect | Skulls in the Stars
Pingback: New theoretical results in the study of extraordinary optical transmission | Skulls in the Stars