One of my goals in blogging has been to run a series of posts covering the “basics” of optics, namely those concepts that form the basis of an understanding of the more advanced topics investigated by researchers today. Though I’ve done a pretty good job so far, I recently realized that I’ve left out a discussion of the most important tool of the optical scientist, and one of the most important technological advances of the modern era: the laser!

Image via Wikipedia, of an experiment at the Air Force Research Lab.
“Laser” is an acronym for “Light Amplification by Stimulated Emission of Radiation”, and it refers to a device that produces light by an unusual physical process not typically found in nature.
In fact, 2010 marks the 50th anniversary of the laser, as the first functioning device was built in 1960 by Theodore H. Maiman at Hughes Research Laboratories in California. To draw attention to this anniversary, optics organizations have instituted a yearlong celebration called LaserFest, and many special events are planned and have already taken place; my favorite being the Lasers Rock! concert that was held in May at the CLEO/QELS conference:
Musical group “Second and Third Harmonic Generation” playing at Lasers Rock! Picture via Ksenia’s CLEO/QELS blog.
I hardly need to describe the impact lasers have had on our society, and it is hardly possible to list all of the applications! Among other things, lasers are used to read CDs, DVDs and Blu-ray discs, they form the basis of the fiber-optic communications systems by which you are probably reading this post, they are used in medicine both to diagnose problems as well as to perform laser surgery, they are used to cut material in industrial fabrication. Their properties make them ideal for doing optics research of all sorts, and they are now an essential tool for researchers.
In this post I would like to describe the physics of lasers. This is no mean feat, because there is a lot to say about how they work, and many variations on the fundamental idea that was first proposed by Charles Townes in the 1950s¹. I will proceed somewhat carefully:
- First, I will discuss what a laser is, and what properties a laser has that distinguishes it from “ordinary” light sources like light bulbs.
- Second, I will describe the fundamental physics behind the lasing effect, in particular the process of stimulated emission.
- Finally, I will explain the engineering that is used to take advantage of stimulated emission and make a laser.
Let’s take a look…
What is a laser? Lasers are sources of light that, by virtue of the physics of their operation, generally possess a number of characteristics that “ordinary” sources of light do not possess. Among these characteristics are:
- Directionality. An ordinary light source, like a light bulb, radiates light in all directions. The light emitted by a laser all travels essentially in a single direction. Diffraction effects eventually cause the laser beam to spread, but it can travel great distances before that happens. The directionality of a laser makes them ideal as an optical (laser) pointer: a small, bright spot of light can be shined across a room without a loss of intensity.
- Monochromaticity. Ordinary light sources tend to emit light over a broad range of frequencies (colors). Lasers tend to produce light that is highly monochromatic (single color).
- Spatial coherence. As has been discussed in a previous “basics” post, spatial coherence is the ability of a wavefield at two different points in space to create interference patterns. Light from an ordinary light source and the Sun is highly incoherent: it is not possible to directly use light from such sources in an interference experiment like Young’s double slit experiment. Lasers tend to produce light that is spatially fully coherent — it can produce highly visible interference patterns.
- Brightness. One measure of the “strength” of a light beam is the rate at which it delivers energy to a target. A more refined measure of the light beam strength is the power per direction of propagation. Because a laser delivers all of its light in essentially a single direction, it has a very high brightness, typically orders of magnitude higher than any conventional light source. The brightness of even a weak laser pointer makes its beam dangerous to the naked eye; pointing the beam in your eye is essentially dumping all of the energy of the laser beam into a very small region of one’s eye.
We can immediately see the advantage of a laser by considering how Young’s interference experiment would be done before the laser. Young himself did his experiment using the brightest source of light he had available, namely the Sun. However, because sunlight is only spatially coherent over a very small area, he needed to block most of the light coming to his experiment and only allow light from a very small hole to illuminate his experiment:
Only a relatively small trickle of light passes through the hole in the collimating screen, and only a small fraction of that light passes through the double slit screen and arrives at the measurement screen. But the light is broadband (multi-color), so the interference pattern seen on the measurement screen ends up being a rainbow-esque array of colors. If we wanted to see a single bright/dark interference pattern, of the form,
we would also need to filter the sunlight passing through the collimating screen, which would attenuate the amount of light available for our experiment ever further. With a laser, however, we would already have filtered, coherent, directional light, and will be able to see a very bright interference pattern. If we want to demonstrate wave optics effects or apply them to a problem, a laser is a far, far better source of light than any conventional source.
The physics of the laser. So what is the origin of this unusual source of light? To understand it, we need to understand a little about atoms and how they absorb/emit light.
One of the most important early results of the era of quantum mechanics was the 1913 Bohr model of the atom and its implications for light/matter interactions. By that time, it had been known for a century that atoms emit/absorb light only at very distinct, characteristic frequencies. Researchers of the late 1800s/early 1900s bent over backwards trying to explain this observation using known physics, but the real explanation required a leap into the new and inexplicable.
Bohr hypothesized that the electron of a hydrogen atom can only orbit the nucleus with special discrete values of angular momentum, which is equivalent to saying that the electron can only orbit at certain discrete orbital distances and possess certain discrete energies, which are labeled by a principal quantum number .
Part of this model is the suggestion that an atom can only absorb/release energy into light “all at once”, in the form of a light particle (photon). When the electron goes from a higher energy state to a lower energy state
, the energy
of the photon is simply equal to the energy released:
. Einstein had already postulated that the energy of a photon is related to the frequency $latex\nu$ of its oscillation, which means that the frequency of the released photon is given by
, where
is Planck’s constant. Using this model, Bohr was able to explain the observed discrete energy levels of the hydrogen atom, and initiated the quantum theory of matter.
We can graphically describe this relationship between the energy levels of hydrogen and the emitted photons by an energy level diagram such as the one that follows, from ThinkQuest:
The horizontal lines represent the energy levels of hydrogen, while the vertical arrows represent the transition of the electron from a higher energy state to a lower energy state with the release of a photon. The process of the absorption of light works in reverse — the absorption of a photon of wavelength 121.57 nm, for instance, will coincide with a transition of the atom from the to
level of the atom. The
state is known as the ground state of the atom; it is the lowest energy state that the electron, and hence the atom, can be in. We can draw energy level diagrams for other atoms and molecules that are of a similar nature — albeit much, much more complicated.
The ordinary process of atomic emission is known as spontaneous emission: an atom in an excited state will, eventually, spontaneously emit a photon and drop to a lower energy state. We have also noted that an atom can also absorb a photon of the proper frequency, raising the atom to a higher energy state.
It was noted by none other than Albert Einstein that a third possibility must exist — it must also be possible for a passing photon to interact with an already excited atom and cause the atom to emit its own photon! This process is what is known as stimulated emission. The three processes are illustrated using energy levels below:
Ordinary light sources are, in essence, a collection of atoms that are excited thermally or electrically and radiate via spontaneous emission. Because the atoms are radiating independently, the light goes in all directions and has a low spatial coherence.
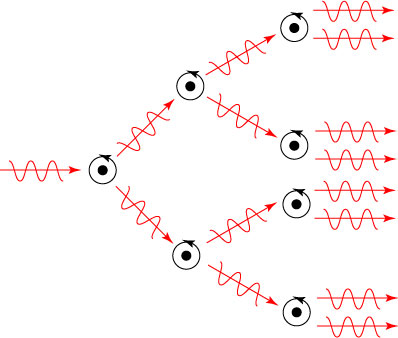
The light radiated by stimulated emission is of a radically different character. The photon released in the process ends up traveling in the same direction as the stimulating photon, and is in essence the two photons are duplicates of one another. This raises an interesting possibility — if each of the two photons leaving the atom in stimulated emission stimulate other atoms to emit, and the process continues, we will have a veritable “avalanche” of photons, all pretty much identical to one another:
This is the basic physics behind the operation of the laser — if we have enough atoms in the excited state, we can generate a massive flood of photons all traveling in the same direction and otherwise behaving identically!
There is an important catch to this, however — how do we get a bunch of atoms in the excited state to begin with? In order for an “avalanche” to be triggered, there have to be more atoms in the excited state than in the ground state, a situation known as population inversion (the “population” of atoms must be mostly in the excited state, “inverted”).
Imagine that we try to create a population inversion by starting with a bunch of atoms in the ground state and excite them with a beam of light of the appropriate frequency. At first, most photons will be absorbed by the atoms and transition to their excited state; however, as more and more atoms get excited, it becomes more and more likely that a photon will instead “kick” an atom back into the ground state. Roughly speaking, when 50% of the atoms have been excited, a photon is just as likely to knock an atom back into the ground state as it is to pump an atom into the excited state. It would seem, using this simple strategy, that it is impossible to get more atoms in the excited state than exist in the ground state.
However, there are more than two energy levels in any atom or molecule! (Refer again to the hydrogen energy level diagram above.) Suppose we simultaneously consider three atomic energy levels, as shown below:
We further suppose that such a 3-level atom that is excited to level 3 very quickly decays to level 2, but the atom takes a relatively long time to decay back to the ground state, level 1. If we excite a collection of these atoms to level 3 using a light beam at frequency , they will drop to level 2 too fast to be de-excited by the light beam! Any atoms still in level 1 can then be also excited to level 3, and so on. By this process, we end up with most of the atoms continually in level 2, and almost no atoms in level 1: we have achieved population inversion!
We can make an even better laser with an appropriate choice of 4 energy levels of an atom, and the realization that we can achieve a population inversion between any two levels of an atom, and the bottom one does not necessarily need to be the ground level. We consider an atom of the form:
We imagine that the atom transitions very quickly from level 4 to level 3, and also from level 2 to level 1. If we are interested in achieving population inversion between levels 2 and 3, we note that such atoms will almost never be in level 2, because it decays so fast — we effectively achieve population inversion once we get any atoms into level 3!
Clearly, not just any 3 or 4 levels of an atom will work — only certain energy levels of certain materials possess the right energy level structure to make population inversion. However, there has been enough research done through the years that an amazing variety of materials have been used as the basis of a laser: solids, liquids and gases alike.
The components of a laser. A laser is more than stimulated emission — a number of components are required to make a laser beam with all the desirable characteristics we introduced above. In fact, the “avalanche” of photons we described above is a distinct phenomenon with its own name, amplified spontaneous emission: an initial photon created by spontaneous emission produces many more photons by inducing stimulated emission in excited atoms.
So what makes a laser? In simplified form, a true laser consists of four components, listed and illustrated below:
- gain medium. The gain medium is the lasing material, to be population inverted, typically a 3-level or 4-level atom. The properties of the laser light such as wavelength depend on the choice of medium.
- optical pump. We need some technique to excite the gain medium into an inverted state. The most obvious technique to do this is to use an optical pump (like a flashbulb) that produces light that can excite the gain medium to the 3rd (or 4th) level. It is also possible to excite the gain medium by electrical means, and even to use another laser as a pump.
- resonant cavity. We discuss the cavity in more detail below. The simplest cavity imaginable consists of two parallel mirrors that bounce the stimulated photons back and forth through the gain medium. On each pass through the cavity, a single photon may excite a large number of additional photons through stimulated emission. The cavity, therefore, gives each photon a large number of opportunities to excite additional photons, enhancing the “avalanche” effect.
- output coupling. Once we get all these photons bouncing around in the cavity, we need to get them out somehow! Typically one of the mirrors is partially reflecting, so that some small, small fraction of photons incident upon the mirror actually pass through it and become the output beam.
The cavity is a fundamental component in producing the directionality and the monochromaticity of a laser. Because the mirrors are nearly parallel to one another, photons that are traveling perpendicular to the mirrors stay the longest in the cavity and therefore produce the most amplification:
The result is that the perpendicularly-traveling photons get the most amplification, and the light beam that comes out of the laser cavity consists primarily of these single-direction photons!
The cavity also acts as a Fabry-Perot cavity, which I’ve discussed previously. Only waves of certain wavelengths, and hence frequencies, will constructively interfere outside of the cavity:
Because the cavity restricts the output light to lie within certain very narrow frequency ranges, the output is very monochromatic.
These are the components that make up a “standard” laser. It is to be noted, however, that scientists and engineers have changed any and all of them to produce a variety of different effects. A discussion of these changes, and their effects, takes us well outside of the “basics” level of this post!
***************************************
¹ The idea of the laser was sufficiently “out there”, in fact, that the idea met with a lot of resistance! I heard a talk by Charles Townes, the visionary who conceived of the idea of the LASER and its microwave analogue, the MASER, a few years ago. Townes described how he discussed his idea with many of the geniuses of his time, and was told by most of them, “It can’t work!” (Some of them later came back to him and said, “Hey, you might be right.”) Also, the paper describing the first operating LASER, by Theodore Maiman, was actually rejected by Physical Review Letters!













Stimulated emission – tee hee! (ok, couldn’t help the 4th grade joke). Keep the basic posts coming, this is great!
Thanks! Yeah, “stimulated emission” was a term coined in an era before pretty much anything could be made to sound filthy…
But . . . How do you attach them to the sharks?
Seriously, though
Thanks for posting this in such a way that a 55 year old w/a degree in history could understand it.
Strangely, the NSF has never wanted to give me funding to find out! 🙂
Maybe you just have to ask the right way.
My grant writing skills are rusty, but something like:
Determining the optimal placement of a series of coherent light sources emitting light of in-step waves of identical frequency, phase, and polarization in the range of 100–3000 W (peak output 1.5 kW) on a viable member of the species of Carcharodon carcharias. Said placement to include a moisture impervious energy source, housing for the light emitting sources and programmable control module.
That actually reads pretty well! The only thing missing is the insertion of the word, “frickin” somewhere, probably in front of “coherent light sources”. 🙂
How does it happen that sunlight is coherent over a small area?
From what you describe the obvious choice is somehow you get stimulated emission. Could there be some other reason? How could the stimulated emission work?
Are, say, incandescent light bulbs coherent over small areas?
I think you’ve seen my post on coherence now; the increase in spatial coherence is, in essence, a geometric effect. Point sources are coherent, and though a large thermal source isn’t, it “looks” like a point source when you get far enough away.
In principle, light bulbs are also coherent over a small area; however, it is a *very* small area.
Thank you, that’s what I’m trying to imagine.
Light from a single atom should be coherent, if it means anything to talk about coherence in that case.
Perhaps light from a single atom starts stimulated emission to get more light total?
It should be possible to estimate how much of the sun is involved in the experiment. Figure out what distance on the screen is relevant. Maybe a centimeter 3 meters distant from the slit or pinhole?
Then the corresponding distance from the center position on the sun would be 1/300 times 150 million km? No, I only included the distance from the second slit to the screen. I need the distance from the first pinhole to the screen.
Still, it seems like it could be a pretty big area for stimulated emission to operate over, right?