Most people, even non-scientists, are aware these days of the notion that light acts sometimes like a wave, sometimes like a particle, depending on the circumstances. This wave-particle duality is a fundamental aspect of nature, applying to all elementary particles, from light particles (photons) to electrons, protons, neutrons, and the constituent quarks of the latter.

It is a difficult concept to fully grasp, and even today a complete explanation of what this means for physics, philosophically, continues to elude physicists.  But the phenomenon can be demonstrated with light and with matter in experiments that are reasonably well-understood, and in particular Young’s double slit experiment has been used to highlight how the wave properties and the particle properties complement each other.

But when the particle properties of light were first postulated by Albert Einstein in 1905, nobody really had any idea how those particles could be reconciled with the wave properties that had been definitively demonstrated over 100 years earlier.  Naturally, it fell to experiments to help clarify what the heck was going on, and the earliest experiment of this nature was done by G.I. Taylor in 1909, and the results appeared in a paper titled, “Interference fringes with feeble light.”

Taylor’s paper, though it is short (only two pages), is a fascinating look at both the theoretical and experimental challenges in that early quantum era, and in this post we’ll take a look at it and the work that led up to it.

To get started, let’s quickly recap about 100 years of physics history!  Between the 18th and 19th century, it was widely accepted that light consists of a stream of particles, thanks to the detailed experimental work of Isaac Newton, published in his book Opticks in 1704.  Newton convincingly showed — for the time, at least — that known optical phenomena such as refraction (change of direction of light when it enters a medium) and diffraction (spreading of light after passing through a small aperture) could be explained by the way that light “corpuscles” interact with matter.

Newton’s work, combined with his reputation, temporarily put to rest the already long-standing debate over whether light is a wave or a particle.  The wave theory had among its proponents the Jesuit scientist Grimaldi (1618-1663), who in fact performed the first systematic studies of the phenomenon, and the Dutch scientist Christiaan Huygens (1629-1695).

The situation would be reversed almost exactly 100 years later, in 1804, when the British physicist Thomas Young (1773-1829) would present the results of his famous double slit (or two pinhole) experiment, providing strong evidence of the wave theory of light.

An illustration of the experiment is shown below.  The key ingredients are a source of collimated light, a pinhole screen, and an observation screen.  Today, the source of collmiated light would be a laser; back in Young’s time and for a long time after, a candle or lightbulb would be used as the source, and a small hole in a collimating screen would be used to secure a directional (and coherent) beam of light.

At the pinhole screen, the light is largely blocked, except at two pinholes. Beyond the pinholes, the waves spread out, as waves do, and interfere with each other.  In those regions where the waves are wiggling up and down in sync with each other, they combine and produce bright regions, and in those regions where the waves are wiggling up and down opposite one another, the cancel out and produce dark regions.  On the observation screen, this manifests as a series of bright and dark lines.  The way Young himself drew it is illustrated below.

If one uses monochromatic (single-color) light, then the pattern can be described as simple being alternating light and dark lines. If, like Young, one uses multicolor light, the spacing of the pattern is slightly different for each color, and the result is a lovely pattern of colored lines.

Interference was the overlooked ingredient in the earlier work by Grimaldi and Huygens, and the lack of discussion of interference hurt their case that light is a wave phenomenon. But interference can only be explained by a wave theory, and Young’s experiment demonstrated it brilliantly. Analogous interference effects can be seen in sound waves and water waves.

Young’s experiment was the turning point in favor of the wave theory of light which, after some initial resistance, soon became the scientific consensus.  Rapid progress was made after Young’s time, notably the recognition that light is a transverse electromagnetic wave, which was first hypothesized by James Clerk Maxwell in the 1860s.

But the wave theory of light could not convincingly explain a few phenomena. Among them was the photoelectric effect, the observation that, under the right circumstances, light shining on a metal plate can cause electrons to be emitted from that plate.

The photoelectric effect was first observed by Heinrich Hertz in 1887, and a number of aspects of it puzzled physicists of the era. In particular, it was noted that electrons were only ejected from the metal once a critical frequency threshold of light was exceeded, and that the intensity of light only increased the number of electrons released, not their energy.  The wave theory of light could not explain the threshold, and it predicted that the energy of the electrons released should increase with intensity.

In 1905, Albert Einstein finally solved the puzzle by arguing that light acts both as a particle and as a wave.  The energy of an individual particle of light, known as a photon, is proportional to the frequency of the light wave, and individual photons knock individual electrons off of the metal.  However, since electrons are loosely bound to the metal, the energy/frequency of the photon must exceed a certain threshold before electrons are ejected.

Einstein’s insight could be said to mark the true beginning of quantum physics, and Einstein would win the 1921 Nobel Prize in Physics for the discovery.  But in the immediate aftermath of Einstein’s revelation, nobody knew exactly what to make of it all.   If light is a particle, how does one reconcile that with the wave properties? And how, exactly, do particles produce interference patterns like waves?  Nobody was sure.

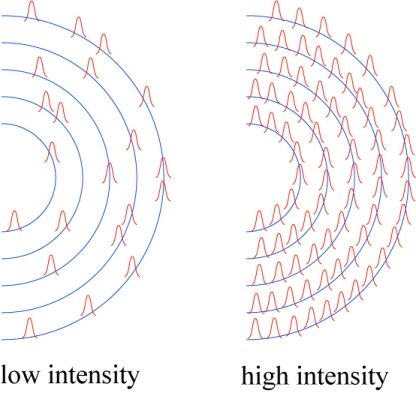
One early thought came from the famed English physicist J.J. Thomson in 1907.  Thomson was studying the ionization of gases through the use of ultraviolet light, which is a similar process similar to the photoelectric effect: instead of visible light kicking electrons off of a metal, ultraviolet light kicks electrons off of atoms.  In trying to reconcile the wave-particle duality problem, he suggested¹ that the particle effects are due to the fact that the actual energy of a wave is distributed unevenly across the wavefront, little “bumps” of energy that are tightly packed when the light intensity is high, and widely spaced when the intensity is low.

Thomson’s model was not particularly well-formed, but the natural implication of it is that the interference pattern produced in Young’s experiment comes from the interaction of many of these little “bumps” of energy. But what happens when only a very small number are interacting with the two pinholes at a given time?  Thomson suggested that the interference pattern must look very different, because there simply aren’t enough bumps around to interfere.

Testing this would be a challenge, however.  Single photon sources of light, common today with advanced lasers and nonlinear materials, did not exist in the early 20th century.  Even if such sources existed, there were not any detectors sensitive enough to detect individual photons, adding to the difficulty of the measurement.

Into this predicament entered the British physicist Geoffrey Ingram Taylor (1886-1975). Born in St. John’s Wood, London, Taylor studied mathematics and physics at Trinity College, Cambridge, from 1905 to 1908, and then obtained a scholarship to continue his work with Thomson.  Thomson’s speculations on the nature of the wave-particle duality was a natural and important research project to undertake, and by January 1909 Taylor had presented his results² to the Cambridge Philosophical Society, “Interference fringes with weak light.”

Taylor’s answer to the problem could be summarized as brute force and patience.  To create a low intensity source, he placed smoked glass screens. Each individual screen would absorb a significant fraction of light passing through them, and screens which were more heavily smoked would absorb significantly more light than those less smoked. It is unclear from Taylor’s description whether he used several screens in conjunction, too; if one screen, for instance, only allows, 1/10th of the light to pass, then two would allow 1/100th, and so forth.  By this method, an arbitrarily high amount of attenuation could be achieved, even to the level where only single photons are illuminating Young’s two pinholes at any time.

The strategy of the experiment was to take five photographic images of Young’s diffraction pattern, each having been exposed to the same amount of total light but having that light pass through the pinholes at different rates. Taylor calibrated his experiment first by taking five photographs of the light source without Young’s pinholes present, and determined how much time was needed for the plates to darken by the same amount; repeating this experiment with the pinholes present, then, one could see how Young’s interference pattern changed when the light intensity was reduced to the level where a small number of energy “bumps” were going through at once.

This experiment required quite a lot of patience. With the pinholes present, even less light was reaching the photographic plates; in order to get sufficient development of the photograph of the dimmest light source, Taylor had to run the exposure for 3 months.

But what did he find? In his own words,

In no case was there any diminution in the sharpness of the pattern although the plates did not all reach the standard blackness of the first photograph.

In short: the interference pattern remained the same, no matter how much the light intensity was reduced.  Taylor and Thomson seem to have initially interpreted this result as indicating that they had not used a dim enough light source to see the effect they sought, and estimated the maximum energy of a single photon from their arrangement. This estimate turns out to be much too small, however, because the explanation of Young’s experiment, and what a photon does in it, is very different from Taylor and Thomson’s vision.

A satisfactory answer would not be found for quite a few years, until after quantum physics had been formulated. Today, we understand the wave-particle duality as follows: each photon travels through the two pinholes as a continuous wave, in a sense passing through both pinholes together.  But the amplitude of this wave is simply related to the probability of a particle being found at a particular point in space; when the particle’s location is measured, such as by the observation screen, it “chooses” which location it appears.

An individual photon will therefore appear as a pointlike spot on a detector screen.  But, as particles are more likely to appear where the wave amplitude is high and less likely to appear where the wave amplitude is low, as photons accumulate on the screen, they will build up to form the familiar Young’s interference pattern.

In Taylor’s era, it was not possible to measure this slow buildup of photons at a detector, but starting in the 1960s researchers were able to measure the same effects using electrons, rather than photons.  One particularly elegant demonstration was done in 1989 by a group of Japanese researchers³, and the buildup can be seen in their results shown below.

As more and more electrons arrive, the pattern of bright and dark bands becomes clear!  The experiment has also been repeated many times with photons, confirming this basic model for how the wave and particle nature of light and matter are reconciled with one another.

It should be noted that, on a deep philosophical level, we still to this day don’t really know what this means. Is the world inherently random, as the probabilistic interpretation of Young’s experiment seems to suggest? Or are there other unseen factors at play that only make it seem random?  Nobody knows entirely for certain.

But Taylor’s work was one of the earliest attempts to reconcile the seemingly paradoxical wave-particle duality, and it is still cited as an important milestone in the history of quantum physics.

***********************************

¹ J.J. Thomson, “On the ionization of gases by ultra-violet light and on the evidence as to the structure of light afforded by its electrical effects,” Proc. Camb. Phil. Soc. 14 (1907), 417.

² G.I. Taylor, “Interference fringes with weak light,” Proc. Camb. Phil. Soc. 15 (1909), 114.

³ A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki and H. Ezawa, “Demonstration of single-electron buildup of an interference pattern,” Am. J. Phys. 57 (1989), 117-120.