Optics basics: Young’s double slit experiment

Posted on March 28, 2009 by skullsinthestars

As I’ve so far been restricting my ‘optics basics’ posts to discussions of fundamental concepts related to optics, it might seem strange at first glance to dedicate a post to a single optical experiment. What will hopefully become clear, however, is that Young’s double slit experiment is connected to so many basic concepts in optical physics (and still provides surprising new results to this day) that one post is hardly enough to describe all the interesting insights that can be gained by studying the experiment and its implications.

The experiment is named for its inventor, Thomas Young (1773-1829), pictured below:

Young demonstrated his genius early in life, having learned to read quite well by age 2, and by age thirteen he was well acquainted with Latin, Greek, French and Italian. Later in life he would learn numerous other languages, and would have a hand in attempts to translate the Rosetta Stone (though I have read it argued that he actually left the translation problem worse than when he started).

By the early 1800s, scientists were still convinced of the so-called corpuscular theory of light. Isaac Newton had, nearly 100 years earlier, offered seemingly solid evidence that the manifold observations of light were best interpreted by treating light as a stream of particles. In 1802, however, Young presented a paper¹ in which laid the theoretical foundations for a view of light as a wave, and in 1804, in a paper entitled, “Experiments and Calculations Relative to Physical Optics,” he presented the results² of his famous double-slit experiment, which strongly illustrated the wave nature of light.

So what is the double-slit experiment, and how does it illustrate the wave properties of light? A simple schematic of the experiment is shown below:

A light source is positioned some distance behind a screen A which possesses a pair of closely spaced narrow slits. Light emerges from the pinholes and spreads as spherical waves; the waves overlap, and the interference pattern produced is projected on a measurement screen B. For future reference, we label refer to the position on the measurement screen as ‘x‘.

Young’s own illustration of this wave interference effect is shown below:

From T. Young, “Course of Lectures on Natural Philosophy and the Mechanical Arts,” 1807.

A simulation of the pattern of light which would be observed on the screen B is shown below:

One should see bright lines of light, where the light from the two slits constructively interferes, alternating with dark lines where the light destructively interferes.

We can understand the general principle of Young’s experiment by a basic geometrical argument. Let us assume that our source produces a monochromatic (single-frequency) wave which hits the two slits at the same time, i.e. so that the peaks of the wave arrive at the the two slits simultaneously. The two waves are then said to be in phase with one another. As a reminder, a snapshot of monochromatic wave traveling along a string appears as below:

We now consider what happens when light emerges from the pinholes and travels to the screen B:

Looking at light which travels to point 1 on the measurement screen, light coming from pinhole Q has to travel farther than light coming from pinhole P; therefore light from Q has a phase lag associated with it relative to the light at point P. Light traveling to point 3 results in the opposite case: light from P has a phase lag associated with it relative to the light at point Q. The distance between each pinhole and point 2 is the same, so the light arrives at that point with the same phase.

We can quantify this as follows: provided the distance L between the screens is large, the paths of light from pinholes P and Q to a point on the measurement screen are nearly parallel. The difference in phase can then be calculated using the following figure:

Assuming the two paths meet at the observation screen, light emerging from pinhole Q must travel a distance $d \sin \theta$ farther than light from pinhole P. Assuming monochromatic light of wavenumber $k$ , this means that the light from the two pinholes arrives at the screen with a relative phase difference:

$\phi = kd\sin\theta$ .

Two waves are out of phase, and produce destructive interference, when this phase is an odd multiple of $\pi$ , i.e.

$kd\sin\theta = (2n+1)\pi, \quad n = 0,1,2,\ldots$ ,

and produce constructive interference when the phase is an even multiple of $\pi$ , i.e.

$kd\sin\theta = 2n \pi, \quad n = 0,1,2,\ldots$ .

A little more geometry demonstrates that $\sin\theta \approx x/L$ , so that bright fringes occur at positions

$x = 2n \pi L/kd$ .

The distance between two successive bright fringes on the screen is given by:

$\Delta x = 2\pi L/kd$ .

It can help to put some numbers into this equation and see what it implies about the size of fringes. Let us assume we have green light, $\lambda = 550 \times 10^{-9}$ meters, and an observation screen $L = 1$ meter from the slit screen. This gives $k = 1.1 \times 10^{7}$ 1/meters. If we assume a slit separation of 1 mm, this results in a fringe separation of

$\Delta x = 0.5$ mm!

If we decrease the separation of the slits to 0.5 mm, we increase the fringe separation to 1 mm. It is clear, though, that the slits must be very closely spaced together in order to observe sizable fringes; there is another coherence-related reason to have closely-spaced slits which we mention in a moment.

It is worth noting that a “double slit” experiment does not necessarily involve using slits at all! The principle of the experiment is the division of a wave in space into two distinct parts which are then brought together to interfere. Young himself performed his initial experiments by placing a piece of thin card into a beam of light and examining the shadows produced on a distant wall. The card was approximately 1/30th of an inch in width. Young also did not have the luxury of using monochromatic light: his interference experiments used sunlight, and the fringes produced were not light and dark bands but fringes of alternating color.

Young’s experiment could be considered the “tipping point” for acceptance of the wave theory of light. However, it has proven useful in understanding a number of other phenomena, as well, as we will see.

One of the earliest extensions of the “double slit” idea was introduced by Augustin-Jean Fresnel and François Arago, who in 1819 published the results³ of experiments to determine the effect of polarization on the interference of light.

Their article (which I will discuss in more detail in a “classics” post in the near future) was clearly inspired by Young’s work, as they begin with a review of the relevant results of the double slit experiment! They then note that Young had only dealt with unpolarized light or light interfering with the same state of polarization, and they wondered what the result would be if a similar interference experiment was done where the light coming from the two pinholes was orthogonally polarized.

To investigate, they separated a beam of unpolarized light into two orthogonally polarized ones by the use of a rhomboid of Iceland spar (calcite) or an achromatic rock crystal prism. The material is birefringent, which means that different polarizations of light travel at different speeds through the crystal, and are refracted differently. The output of the crystal is two parallel beams. A metal cylinder was placed in between these two beams, partly obstructing each, in the same manner as Young’s cardstock was used to divide sunlight. Part of each beam gets diffracted into the shadow region behind the cylinder, and the wavefield in that region was examined for the presence of fringes:

The result of this initial experiment demonstrated that light beams that are polarized in perpendicular directions do not interfere. Further observations about the relationship between interference and polarization are now referred to as the Fresnel-Arago laws. This experiment was one of the major demonstrations that light must be a transverse wave, i.e. that the vibrations of light waves are perpendicular to the direction of wave propagation.

Returning momentarily to Young’s original experiment, it is to be noted that Young could only see fringes when he performed the experiment with sunlight passing through a very narrow hole:

I made a small hole in a window-shutter, and covered it with a piece of thick paper, which I perforated with a fine needle.

This point-like source of light is necessary because sunlight has extremely low spatial coherence, and interference fringes can only be observed for light of high spatial coherence. Turning this idea on its head, it turns out that Young’s double slit experiment can be used to directly measure the spatial coherence of an illuminating light field.

I have discussed coherence in another basics post, but we’ll review the relevant concepts in order to discuss their relationship to Young’s experiment. Interference effects such as those seen in Young’s experiment require the interfering waves to have a definite phase relationship to one another — that is, if they are in phase at one point in time, they should be in phase for almost all times. Realistic waves, however, are never perfectly monochromatic. Ordinary thermal sources of radiation, such as a lightbulb or the Sun, consist of a large number of atoms radiating light almost independently of one another. The field emanating from such a source has random fluctuations of amplitude and phase. The net result of all these atoms radiating independently is that the wavefronts emanating from a light source are constantly changing their shape — and the more the shape fluctuates in time, the less spatially coherent the wavefield is:

In the left illustration above, the fields at points $P_1$ and $P_2$ are always oscillating in synch: there is a definite phase relationship between the fields at the two points. In the right illustration, the fields at the two points may or may not be in synch – the fields are partially coherent.

One can show (though this involves mathematics outside the scope of a basics post) that the visibility of the interference fringes in Young’s experiment is a direct measure of the spatial coherence of the field at the two slits. The visibility $\mathcal{V}$ of interference fringes is defined as

$\displaystyle \mathcal{V} = \frac{I_{max}-I_{min}}{I_{max}+I_{min}}$ ,

where $I_{max}$ and $I_{min}$ are the brightest and dimmest intensity the wavefield achieves in the neighborhood of a single bright interference fringe. If there are no fringes, i.e. no spatial coherence, the light intensity is uniform, $I_{max}=I_{min}$ , and $\mathcal{V}=0$ . If there is complete destructive interference, $I_{min}=0$ and $\mathcal{V}=1$ . The visibility of the interference fringes are a direct measure of the spatial coherence of the wavefield: when $\mathcal{V}=0$ , the field is incoherent at the two slits, and when $\mathcal{V}=1$ , the field is fully coherent. In essence, Young’s experiment is the archetypical technique for measuring the spatial coherence of a light wave.⁴

We have seen how Young’s experiment was originally used to demonstrate the wave properties of light. In an ironic twist, it is now used quite regularly to show not only the wave-like properties of matter, but also the particle-like properties of waves!

Historically, the latter of these concepts was the first to appear. With this in mind, a little historical background is in order. By 1900, although Newton’s corpuscular theory of light had been discarded in favor of a wave theory of light, “cracks” in the wave theory began to appear. Perhaps the most significant of these was the photoelectric effect, in which light illuminating a metal surface ejects electrons from that surface. Wave theories of light could not seemingly account for the observed properties of the photoelectric effect, and in 1905 Einstein suggested that the experiment could be readily and easily explained if one imagined that light in fact consists of a stream of particles. These particles, later named photons, of course also possessed wave-like properties, and this was the first illustration of the idea of wave-particle duality, i.e. that all matter and energy must possess both wave-like and particle-like properties.

Einstein’s interpretation raised interesting questions concerning Young’s interference experiment. If light consists of particles, what, exactly, is producing the interference pattern? If one photon at a time is sent through Young’s interferometer, what will be the result?

The first attempt to answer this second question was undertaken by G.I. Taylor in 1909. Taylor performed the experiment with increasingly dim beams of light, the attenuation being undertaken with a collection of smoked glass screens. Taylor’s “double slit”, incidentally, was produced by looking at the shadow cast by a needle. Taylor recorded his interference patterns with photographic film, and was careful to make certain that the total amount of light falling on the film was the same in each case. For the weakest beam of light, this involved running the experiment continuously for an astounding three months! In such a case, typically one photon at a time would have been passing through the double slits. Taylor found, however, that the interference pattern looked essentially the same in each of his images. Evidently each photon “carries” information about the interference pattern with it, though the exact nature of this relationship would require further discoveries, both experimental and theoretical.

In 1924, Louis de Broglie successfully defended his doctoral thesis, in which he proposed that, in analogy with light, matter must also possess a dual wave/particle behavior. Only three years later, in 1927, Clinton Davisson and Lester Germer proved⁶, essentially by accident, de Broglie’s hypothesis. Davisson and Germer were studying the behavior of electrons when scattered from a crystalline nickel surface. To their surprise, they found that the electrons were preferentially being scattered in certain special direcctions, a result that was already known from X-ray experiments as Bragg diffraction, a wave phenomena. Davisson won the Nobel prize for his work in 1937.

With the wave properties of electrons demonstrated, it was natural to expect that Young’s experiment could be done with electrons, as well. This was finally done in 1964 by Claus Jönsson⁷, in an experiment which is now referred to as one of the most beautiful physics experiments of all time⁸. Jönsson etched slits into a thin silver film; the slits were of a thickness on the order of 0.3 μm (μm = 1 millionth of a meter) and were separated by roughly 1 μm. The experiment was done with 1-5 slits; for two slits, he produced the following photograph:

Jönsson, Am. J. Phys. 42 (1974), 4- 11; Figure 8.

This can be seen to be directly analogous to the interference pattern for light shown previously.

By the 1930s, the basic foundations of quantum mechanical theory had been laid. One of the more perplexing aspects of the theory, however, was the measurement problem. In short, the “wave” of a quantum-mechanical particle such as an electron or photon should be interpreted as relating to the probability of finding the particle at that point in space. The wavefunction of the particle therefore follows all possible paths of the particle simultaneously, including going through both slits in the double slit experiment. When the position of the particle is measured, however, it can only be detected at one place: the wavefunction “collapses” on measurement and the particle is detected as a point particle. The likelihood of finding the particle at a particular point can only be described probabilistically.

(If this doesn’t really make sense to you, you’re not alone; the measurement problem is one of the still-unresolved questions of quantum mechanics. We can say, however, that even though it doesn’t completely make sense, it works perfectly well in interpreting experiments.)

What does this mean? If we were to perform an experiment with a single electron/photon, and I really mean just one electron/photon, we would not see any wave behavior at all. It is fair to say that one cannot detect any wave properties of a single particle in isolation. When we repeat the experiment many times, we will notice that the particles tend to appear more often at some places (regions of constructive interference) and don’t appear very often at other places (regions of destructive interference). If we can fire a single electron/photon at a time through a double slit experiment, and keep track of where we detect them, we will see the classical wave interference pattern ‘build up’ over time.

In 1976, three Italian researchers Merli Missiroli and Pozzi performed this exact experiment⁹, and recorded the creation of an electron interference pattern on a television monitor. The results of their experiment are shown below:

This picture was actually taken by looking at the image on a television monitor for differing intensities of electron beams, but the researchers also developed a similar picture by looking at the cumulative effect over time of a large number of electron detections. In essence, individual electrons appear as points on the detector, but over time one sees that they distribute themselves according to the classical double slit interference pattern.

This experiment was repeated in 1989 by a Japanese research group¹⁰, with more advanced equipment and even more spectacular results:

Perhaps even more fascinating is the less-often reported comparable experiment with photons. Just like electrons, photons can only be detected at a single point, and an interference pattern with light is built up by a large collection of discrete photon detections. A lovely example of this experiment is depicted in the paper by Dimitrova and Weis from 2008¹¹.

Young’s experiment continues to produce interesting physical insights¹². We have stated that the interference pattern produced by Young’s experiment can be used to deduce the state of coherence of the light field at the two slits. In recent years, researchers have looked at the spatial coherence of the light in the interference pattern and found that, surprisingly, there exist regions where the light is fully coherent¹³ and fully incoherent¹⁴, regardless of the state of coherence of the light at the two slits.

Young’s experiment has been used to provide insights into nano-optical research, as well. I have previously discussed the relationship between “extraordinary optical transmission” and electric charge surface waves on metal plates known as surface plasmons. Early experiments in the field, and their interpretations, were somewhat contradictory, and this led to a heated debate about the exact role of surface plasmons in extraordinary transmission. The confusion was cleared up somewhat when, instead of studying transmission through a large array of holes, researchers studied the transmission through only a pair of holes, essentially Young’s experiment with surface plasmons¹⁵. More recently, it has been shown that the presence of plasmons can affect the coherence properties of light in Young’s experiment as well¹⁶.

Thomas Young’s experiment has proven persistently useful because it boils down interference phenomena into their most fundamental form: the interference of two spatially separated waves. I would not be surprised to see yet more new physical insights arise from Young’s simple but powerful idea. (And I’m sure I’m forgetting at least a few interesting results which can be derived from it!)

1. T. Young, “On the Theory of Light and Colours,” Proc. Roy. Soc. Lond. A 92 (1802), 12-48.

2. T. Young, “Experiments and Calculations Relative to Physical Optics,” Proc. Roy. Soc. Long. A 94 (1804), 1-16.

3. F. Arago and A. Fresnel, “Sur l’Action que les rayons de lumière polarisés exercent les uns sur les autres,” Ann. Chim. et Phys. 10 (1819), 288-305.

4. See, for instance, the relatively recent book by E. Wolf, Introduction to the Theory of Coherence and Polarization of Light (Cambridge University Press, Cambridge, 2007).

5. G.I. Taylor, “Interference fringes with feeble light,” Proc. Camb. Phil. Soc. 15 (1909), 114-115.

6. C. Davisson and L.H. Germer, “Reflection of electrons by a crystal of nickel”. Nature 119 (1927), 558–560.

7. C. Jönsson, Zeitschrift für Physik 161 (1961), 454. Reprinted in English as “Electron diffraction at multiple slits,” Am. J. Phys. 42 (1974), 4- 11.

8. R. Crease, The Prism and the Pendulum: The Ten Most Beautiful Experiments in Science (Random House, New York, 2003).

9. P.G. Merli, G.F. Missiroli and G. Pozzi, “On the statistical aspect of electron interference phenomena,” Am. J. Phys. 44 (1976), 306-307.

10. A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki and H. Ezawa, “Demonstration of single-electron buildup of an interference pattern,” Am. J. Phys. 57 (1989), 117-120.

11. T.L. Dimitrova and A. Weis, “The wave-particle duality of light: A demonstration experiment,” Am. J. Phys. 76 (2008), 137-142.

12. Full disclosure: I know very well the authors of the following papers, which is of course why I am aware of them!

13. H.F. Schouten, T.D. Visser and E. Wolf, “New effects in Young’s interference experiment with partially coherent light,” Opt. Lett. 28 (2003), 1182-1184.

14. H.F. Schouten, G. Gbur, T.D. Visser and E. Wolf, “Phase singularities of the coherence functions in Young’s interference pattern,” Opt. Lett. 28 (2003), 968-970.

15. H.F. Schouten, N. Kuzmin, G. Dubois, T.D. Visser, G. Gbur, P.F.A. Alkemade, H. Blok, G.W. ‘t Hooft, D. Lenstra and E.R. Eliel, “Plasmon-assisted two-slit transmission: Young’s experiment revisited,” Phys. Rev. Lett. 94 (2005), 053901.

16. C.H. Gan, G. Gbur and T.D. Visser, “Surface plasmons modulate the spatial coherence in Young’s interference experiment,” Phys. Rev. Lett. 98 (2007), 043908.

This entry was posted in Optics, Optics basics. Bookmark the permalink.

48 Responses to Optics basics: Young’s double slit experiment

IronMonkey says:

March 30, 2009 at 8:54 am

Thanks again for a very instructive post. It truly shows how Young’s double slit experiment is one of the most basic yet insightful method to study wave-particle physics. It was also nice to see an original drawing used by Young!

Reply
- skullsinthestars says:
  
  March 30, 2009 at 10:51 am
  
  IM wrote: “It was also nice to see an original drawing used by Young!”
  
  One of the nice things about historical papers like Young’s are the lovely figures they contain. Figures like Young’s are really works of art, which probably comes about because of the amount of time they had to spend producing their figures. Not that I’d want to go back to an era without Illustrator…
  
  Reply
Blake Stacey says:

March 30, 2009 at 10:24 am

The books I’ve read on the deciphering of hieroglyphics generally say that Thomas Young made some real accomplishments, although he didn’t get nearly as far as Champollion: he worked out the values of a few alphabetic signs, correctly identified cartouches as containing royal names, etc. Of course, the history in the first chapter of a hieroglyphics book may well contain its own “textbook cardboard”!

Reply
- skullsinthestars says:
  
  March 30, 2009 at 4:36 pm
  
  Blake: My impression is similar to the one you got from your reading, but I felt like making a more conservative statement to “cover all the bases!”
  
  Reply
Kaleberg says:

March 30, 2009 at 10:13 pm

My favorite slit experiments involve using a single photon to tell if one of two pathways are blocked, without sending a photon down the blocked pathway. Basically, if the photo just goes straight through one of the slits, then the other is blocked. If it winds up somewhere random, then neither slit is blocked. (Of course, the photon might just happen to follow a straight path even with two unblocked slits, but this is rather unlikely.) How does the photon know that the other slit is blocked? That’s one of the great mysteries.

Reply
Pingback: pligg.com
Andy Stuart says:

April 9, 2009 at 2:19 pm

Hello from Kelowna,

Reading your Young’s Double Slit Experiment article where you make reference to “wavenumber k”

I looked it up in a physics dictionary where I found that it is defined as follows: k = 2pi/lambda. The magnitude the angular wave vector or, propagation vector.

If my thinking is right the pi units are radians/rev and lambda, the wavelength is cm/rev. The ratio being radians/cm. Some kind ratio of curvilinear distance and linear distance.

Still not telling me anything.

Could you elaborate on how you think of k?

Much appreciate your set of blogs.

Andy Stuart

Would you kindly elaborate on what k is

Reply
- skullsinthestars says:
  
  April 9, 2009 at 3:59 pm
  
  Andy: In a previous ‘basics post‘ I described the basic wave quantities in some detail. To some extent, wavenumber ‘is what it is’: a different, sometimes more convenient, way of writing the wavelength.
  
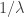  Otherwise, it can help to think of it by using a specific example: suppose the wavelength $\lambda = 1/5$ meter. Then, over a distance of 1 meter, the wave repeats itself 5 times, or (number of times wave repeats in 1 meter) = $1/\lambda$ = 5. Since each repeat of the wave consists of 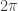$2\pi$ radians ‘around the circle’, the number of radians which appear over the distance of 1 meter is
  
  $k = 2\pi /\lambda$ .
  
  Reply
Pingback: Physics Shirt | Schrodinger’s LOLcat | The Nerdiest Shirts
Pingback: XiXiDu’s News » A Guide to Quantum Physics – A Few Links
b.kittu says:

September 12, 2009 at 8:11 am

what is digital electronics

Reply
J Thomas says:

October 9, 2009 at 9:55 pm

In your simulated interference pattern shown just below Young’s illustration, I notice a pattern. There is a thick white line with then gray areas around it. To the right there is a thin white line offset to the right, with a wide gray area to the left and a narrow gray area to its right. Then there is a thin white line offset to the let with a wide gray area to the right and a narrow gray area to its left. Then the pattern repeats.

But I did not see that in the Jonsson photograph of an interference pattern.

Why is this? Does the simulation simulate something which is always or sometimes present but not always easy to see?

Reply
- skullsinthestars says:
  
  October 9, 2009 at 10:15 pm
  
  J Thomas: Hmm… I hadn’t noticed that before! I believe that it is an artifact of the plotting software used in my simulation. Basically, the software is only calculating the intensity of the field at discrete points of the field and then interpolating to determine the function in between. I probably used a small number of discrete points, which sometimes were closer to the true maxima (making the brightest, thickest lines) and sometimes farther away (resulting in dimmer, narrower lines). If I redo the simulation and calculate the field with more points/mm, it should look more like the Jonsson pic.
  
  Reply
  - J Thomas says:
    
    October 10, 2009 at 7:10 pm
    
    I want to encourage you to do that.
    
    It’s possible that your simulation is showing something real that is hard to see. I notice that with most pictures of interference patterns I see wide bands of alternating light and dark areas with thin lines of cancellation between them. I’m reasonably sure this is because my eye does not see something twice as light and twice as dark as all that different, I see intensity on more like a log scale, and so I don’t see half the area as more-than-average and half of it as less-than-average. I see waves everywhere with thin gray areas.
    
    So if something like your plotted graph was actually going on, I would probably miss it when I look at real diffraction patterns or water-wave pictures.
    
    When I look at pictures of interference patterns it looks like, when bands of constructive interference head toward the flat screen, all but the center one are tilted somewhat. They are heading in different directions, at increasing angles.
yoron says:

February 25, 2010 at 8:41 pm

I’m getting more and more impressed over your efforts to understand and interpret photons and waves. A very good work.

Reply
Eyal Shahar says:

October 13, 2010 at 12:29 pm

I have read many descriptions of the slit experiments and the explanation for the particle-wave duality. Your is one of the clearest. Thanks!

One comment and two questions, with your permission.

Comment: why is the single-slit experiment not described? The interference phonemena is evident in this simpler model. Have I missed it in the text, or is the single slit perceived as variation of a double slit?

Questions:
1. Quote: “When we repeat the experiment many times, we will notice that the particles tend to appear more often at some places (regions of constructive interference) and don’t appear very often at other places (regions of destructive interference).”
Comment: Don’t we observe this phenomenon on the macro scale as well? When I narrow the opening of a garden hose with my thumb, I observe constructive interference and destructive interference of the water. The emerging stream is clearly separated into alternate regions of “more particles” and “less particles”.

2. The emphasis is usually placed on the width of the slit, which should be narrower than the width of the light beam. I have been wondering about the impact of the “thickness” of the slit, namely, the length of the path that the light travels within the slit. For example, suppose the slit is created by cutting a thin opening in a piece of metal which is 0.5 cm thick rather than in a piece of metal which is 0.01 cm thick. Does it matter with respect to interference and the related math of waves ?

Again, many thanks for a great blog.

Reply
- skullsinthestars says:
  
  October 13, 2010 at 2:15 pm
  
  Thanks for the comment, and questions! I’ll try and respond this evening…
  
  Reply
- skullsinthestars says:
  
  October 18, 2010 at 10:27 am
  
  Thanks for commenting! To answer your questions:
  
  1) “why is the single-slit experiment not described?” The single slit experiment is typically considered a diffraction experiment, not an interference experiment. Nowadays the two effects would be considered more or less interconnected, but in Young’s time diffraction had been observed for hundreds of years but direct interference of waves had not. I talk about diffraction separately in another “optics basics” post.
  
  2) “Don’t we observe this phenomenon on the macro scale as well?” The garden hose example you give is not, in fact, an example of interference. The different streams of water that you observe have to do more with the turbulent nature of the water when it is squeezed through the smaller opening. One place where interference can be seen on the macro scale is with sound waves — two sources of sound that are in phase with one another will produce regions of constructive and destructive interference, where sound will be louder or softer, repsectively.
  
  3) “I have been wondering about the impact of the “thickness” of the slit, namely, the length of the path that the light travels within the slit.” That’s a good question, and it can make a huge difference on the behavior of transmitted light. The thickness typically only comes into play, however, when the width of the slit is smaller than the wavelength of light. This is the domain of so-called “nano-optics”, the study of light interactions on subwavelength scales, and it is an interesting field of study in large part because things such as the thickness of the metal plate become important.
  
  Reply
RAMESH says:

October 20, 2010 at 2:41 am

This is very clear,i can understad simple.thank you

Reply
John R (Jack) Smies says:

December 10, 2010 at 6:09 pm

Seems I’ve seen reference to Freznel and Huygens commenting on a background field being a possible explanation of the double slit results. Any validity to this theory?

Reply
- skullsinthestars says:
  
  December 10, 2010 at 10:12 pm
  
  Hmm… haven’t heard anything about such an explanation; I’ll have to look into it!
  
  Reply
piyush pratik says:

May 26, 2011 at 8:44 am

i cannot understand how the total no. of maximas are counted…………..i alwaz get confused ………..please tell me how to do that………

Reply
- skullsinthestars says:
  
  May 26, 2011 at 11:38 am
  
  Could you be a bit more specific? I’m not sure what you mean by the “total number” of maximas. In principle, there are an infinite number spread out across the measurement plane, with a certain density of maximas per unit length.
  
  Reply
Ouroboros says:

September 25, 2011 at 9:41 pm

If time could be thought of as a separate dimension(s) might it be possible for a thing to exist almost entirely in time (a wave) and intersect only very briefly with space at singular points (particles)? The science is beyond me. No less curious, all I can do is look beyond the science.

Reply
adibahnabilah says:

December 2, 2011 at 7:44 pm

i want to ask u…
1) if the double slits is separation of d is increases what would happen to the separation distance between two onsecutive bright bands???
2) if we use laser light green what wuold happen to the separation distance between two consecutive bright bands???

Reply
- skullsinthestars says:
  
  December 2, 2011 at 7:50 pm
  
  As you increase the slit separation, the separation between bright bands decreases.
  
  Green light is what I used in the example! What you may be asking: as wavelength increases, the separation between bands increases.
  
  Reply
  - adibahnabilah says:
    
    December 3, 2011 at 7:09 am
    
    thank you skullsinthestars 🙂
- J Thomas says:
  
  December 2, 2011 at 8:17 pm
  
  If you assume that light travels in waves, and the waves can interfere, then the math is easy. Just do the math and get the answers.
  
  Here’s a link that gives a condensed explanation.
  http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/fraunhofcon.html
  
  Reply
rbha says:

May 17, 2012 at 4:11 am

what happend if a glass slab is placed in path between slit and screen

Reply
- skullsinthestars says:
  
  May 18, 2012 at 9:51 am
  
  If the slab is placed in front of one slit, and we can ignore reflection, then it slows the light traveling through it, introducing a phase difference between the light emanating from the two slits. The result of this difference is that the interference pattern shifts as a whole along the screen!
  
  Reply
- sarath says:
  
  March 24, 2016 at 10:42 pm
  
  If you place a glass in between slit and screen the possision of dark and bright and is changed
  
  Reply
Dan Local realist says:

June 29, 2012 at 7:18 am

What say the two slit effect arises because the photon is simply an (for some reason) indivisible wave form having enough lateral extension to propagate through both slits. Provided the centre of the photon, which would after all be its centre of momentum and influence, found a slit the remainder of the photon might then be drawn through the barrier. This would be akin to a test charge on side of a barrier having an influence on the other. Those parts of the wave passing through a slit would retain mutual coherence, but the remainder would suffer various degrees of dephasing as a result of interference from induced effects in the material of the barrier. The paths of constructive interference – those paths along which the photon most easily retained the coherence of its characteristic transverse wave for would thus be determined (as is observed) by the geometry of the slits.
Why should not the individual photon have the required lateral extension. Such extension is assumed in standard quantum mechanics of the associated probability wave. The HOM experiment demonstrated a longitudinal extension for the photon of several hundred effective wave lengths, and a similar lateral extension might be supposed on the same basis.
This wouldn’t explain interference of the Mach Zehnder variety, but nor is that the same variety of self interference.

Reply
- J Thomas says:
  
  June 29, 2012 at 11:29 am
  
  There is no problem about interference if you assume the light is a wave. The only problem comes when you assume the light is also photons that are particles. A light wave can be reflected or absorbed by barriers with no conceptual difficulty. The only problem with photons doing that is that each photon is assumed to be a packet of energy, and if you split it up into the part that gets absorbed, the part that gets reflected, and the two parts that travel through two slits, then you have divided your particle into four parts and presumably very little of its energy will be in the parts that travel through the two thin slits.
  
  The wave stuff appears to work just fine. Here is a short description of the math.
  http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/sinvar.html#c2
  They make an approximation that’s usually good enough, and then expand out the correct form given the Fraunhofer simplification assuming a plane wave at the slit.
  http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/fraungeo.html#c1
  
  The reason the math is so complicated is that they use a flat plate to see the diffraction pattern on. If you instead use a curved plate so the distance to the center of the slit is always the same, then the formula for the angle of the first minimum is simple:
  
  (pi/2 – theta) = acos(lambda / a)
  
  where all the symbols are the same as in their illustration, except you don’t calculate y but instead the angle theta.
  
  The only thing that causes problems for light is that atoms are observed to emit quantized amounts of light and absorb quantized amounts of light. But as far as I know, radio towers do not emit quanta of radio waves. Each electron in the antenna that moves back and forth at say 100 times a second goes right on emitting as long as it’s persuaded to move back and forth.
  
  I think more and more that light is much easier to think about if we think of light quanta as a property of atoms, and not of light. I don’t know how to do that with electrons or other particles that do diffraction, though.
  
  Reply
  - J Thomas says:
    
    June 29, 2012 at 5:41 pm
    
    Oops, I found a mistake in my formula. Publishing it gave me the impetus to look closely enough to find it. I think there’s value in using a cylindrical target so the lengths will be more similar, but it doesn’t come out as simple as I hoped.
aliff says:

July 1, 2012 at 4:23 am

if the double slit is replaced by another with slit spacing of d=0.25mm.What would happen to the separation distance between two consecutive bright bands?How to explain it?

Reply
J Thomas says:

August 28, 2012 at 11:47 pm

I worked out the Fraunhofer equation assuming a semicircular screen instead of a flat one. I describe the results here:

http://www.glowscript.org/#/user/jethomas5/folder/diffraction/program/Fraunhofer_diffraction

with diagrams etc. I used GlowScript to do it, which does not work well on old computers, old browsers, or some modern graphics cards. I hope the incompatibilities will get ironed out reasonably quickly.

My version seems simpler to me, and somewhat more intuitive. I can say geometrically just where to expect the

y = lambda D/a approximation to break down.

Reply
md asim says:

July 14, 2013 at 5:50 am

Wht happens whn screen is placed perpendicular

Reply
wayne says:

September 12, 2013 at 7:43 pm

If you fire a coherent light wave at the double slits you get interference. When you fire photons one at a time you also get interference. But how do ensure the single photons are coherent? Or they not have to be coherent? Or am I misinterpreting something?

Reply
J Thomas says:

September 13, 2013 at 7:23 am

Wayne, you’re looking at a question of interpretation.
You can interpret light as waves and some questions are easily answered.
You can interpret light as photons and some other questions are easily answered.

So when you turn on a laser, it makes light that’s mostly coherent because each individual excited atom that releases a photon, releases it at precisely the right time — when passing wave maximum goes by. Notice how I mixed the metaphors? OK, maybe a passing photon gets absorbed and then the atom releases two photons, and there’s essentially no delay when that happens. So the result is that you get coherent light, either photons released at the same time or a single amplified wave.

To prove that it’s photons and not just a wave, you reduce the intensity of the wave after it’s formed down to the point that only one photon is formed at a time. You obviously can’t make a laser work at that intensity, you have to start with a more intense laser beam and then attenuate it to the point that the wave amplitude is less than one photon per time unit.

Now look at the detector, let’s say a photographic emulsion. When a photon hits just the right atom in a crystal, the atom absorbs the whole photon and then the whole crystal changes form into something that results in a black dot on the photo. If the light is a wave that has more than enough energy, the atom could absorb just one quantum and leave the rest. But if there isn’t enough, how could it happen? The light must have been in quanta all along, and they either get absorbed or they do not.

To keep a wave explanation you would have to assume that these atoms are in some sort of probabilistic states, so that sometimes they already have almost enough energy to flip into the other state and sometimes it takes a lot, and the wave has to supply whatever is needed, so the higher the wave amplitude the more often that happens. Or the crystals randomly focus the light and occasionally an atom gets enough. Or some other explanation which is not accepted. The only acceptable explanation is that light always travels as discrete photons. It’s true for laser light that gets emitted one little bit at a time by individual atoms, so it’s probably true all the time.

Each individual photon takes every possible path through the slits and everywhere, but some paths are very very improbable. If they were launched at a slightly different time those paths would not be improbable, other paths would be improbable. So because the photons are in phase, all launched at the same time or a precise time later, they will follow the same paths and will slowly build up a pattern on the film. If they came at slightly different times they would make a different pattern, and both patterns superimposed would look random. It doesn’t matter that the photons go through the slits one at a time, because each one gets its probability distribution all by itself.

Why is it that photons which are emitted with a particular frequency at one particular time will all act one way, while photons which are emitted slightly later, half the frequencyi later, behave very different? I don’t know. But it has been observed to always happen that way, so it must be true.

Maybe there’s a question of interpretation involved.

Reply
wayne says:

September 13, 2013 at 8:41 pm

J Thomas, thanks.
So Its strange that non-coherent photons will not interfere. Has something to do with the wavefunctions adding up and the probabilities. I will to do the math. Even fired single photons have to be coherent.

Reply
- J Thomas says:
  
  September 14, 2013 at 6:40 am
  
  Of course a single photon is coherent with itself. But it maybe gives you a single detection — a single crystal turned black — which doesn’t tell you much, or it goes undetected and tells you nothing.
  
  For the photon model to make sense, each photon must act independently. It must simulate a wave while it travels through two slits etc, and then it must put all its energy in one single place to be absorbed by one atom.
  
  You could imagine that photons interacted. Like, a crystal in the photo emulsion might have a long time after it is ready to change form when another photon could reverse the process. Then photons that go through one slit might somehow interact with those that go through the other even though they don’t do it at the same time. But there are various kinds of light detectors and all the ones that have been tested would have to be slow enough to get the observed results.
  
  So it’s easier to suppose that photons do not interact and photons that are created a tiny fraction of a second later will have a completely different probability function because of the time it is created.
  
  Reply
smarth says:

February 24, 2014 at 9:06 am

what if emanating wavefront is in form of lagging strokes of spheres interrupting the slit p the sourceoints from

Reply
J Thomas says:

September 22, 2014 at 11:55 pm

A few hours ago somebody named “free fetish webcams” offered to write guest articles here, but said nothing about his/her competence in physics or horror writing. Now the comment has been deleted.

It certainly isn’t possible to follow up every possibility, and there are many that are best left unexplored. (There are things man was not meant to know….) But very occasionally, doesn’t curiousity gnaw away at your better judgement?

Reply
akiranick says:

February 28, 2016 at 12:33 am

what would be the the likely cause of the percentage error(s) from the experiment? and how to to reduce the error(s)?

Reply
sarath says:

March 24, 2016 at 10:32 pm

Light is a wave the photos to do the work of the wave . If it make a bright and dark band here there is a collision of two photos in the curve

Reply
Sid Schaudies says:

July 28, 2017 at 5:57 pm

Quoting you above (October 18, 2010 at 10:27) in your reply to Eyal Shahar (October 13, 2010 at 12:29 pm):
“3) “I have been wondering about the impact of the “thickness” of the slit, namely, the length of the path that the light travels within the slit.” That’s a good question, and it can make a huge difference on the behavior of transmitted light. The thickness typically only comes into play, however, when the width of the slit is smaller than the wavelength of light. This is the domain of so-called “nano-optics”, the study of light interactions on subwavelength scales, and it is an interesting field of study in large part because things such as the thickness of the metal plate become important.”

Are you aware of any additional investigations or information occurring within the past 7 years into the role that slit thickness may play ?

Reply
Catherine says:

February 3, 2018 at 2:50 pm

The light wave demonstration was used in Michael Crichtons TIMELINE.

Reply
Jonah Thomas says:

February 4, 2018 at 4:47 am

Photoelectric effect:

When I was learning to walk I had a toy that I could push or pull. When its wheels turned, they bent a spring, and when the spring was bent just enough it would spring back and make a sound.

If I pulled faster the sounds came closer together, but they didn’t get louder. Because the toy was set up so that adding more force couldn’t push the spring farther. It released when it was ready to.

Maybe atoms are like that when they release electrons. Giving them more force doesn’t make the electrons move faster. It just charges more atoms up to the point they release electrons.

The light doesn’t have to be quantized, because the atoms are quantized.

If light acted as a wave there would be no mystery about the double slit experiment at low intensity. Apart from the photoelectric effect, are there reasons to think that light should be particles that exist at one location at a time, instead of waves that are spread over an area?

Reply