Last week was a relatively lousy one for me, but it was made up in part by getting a good question from a student on waves and interference after class. It’s really nice to get a question that indicates a genuine interest in the science (as opposed to just wanting an answer to homework), and I thought I’d discuss the question and its answer as a post.
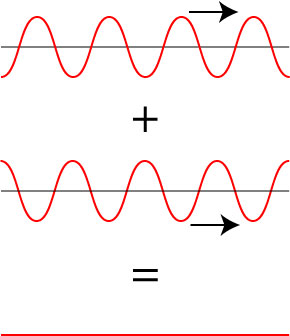
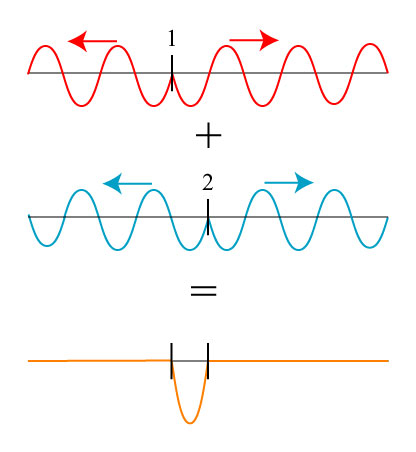
The situation in question is as follows: suppose you have a harmonic wave on a string traveling to the right such that in a snapshot of time, the string looks as follows:
This wave carries energy, and there is a net flow of energy to the right. Now suppose we excite the string with an additional wave of the same frequency and amplitude, but completely out of phase. The sum of the two waves then vanishes:
The two waves cancel each other out, leaving a completely unmoving string due to destructive interference. My student asked me: what happens to the energy? As posed, it seems that we started with two waves carrying energy, but they canceled each other out, leaving no energy! This interpretation cannot possibly be correct, so where is the flaw in our description?
There are actually two aspects to the answer that I want to address, each of which is rather important in the understanding of wave phenomena. The first of these is the observation that the answer to the question depends on how the waves were generated in the first place!
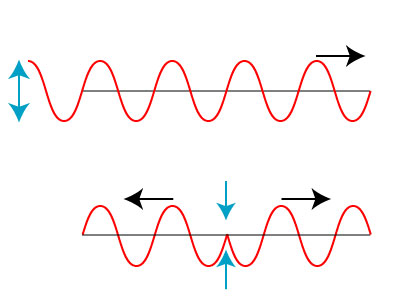
Let us formulate the problem as follows: one wave is generated far away on the left of the string, perhaps by a hand shaking it up and down. The second wave is generated locally at a point on the string by some sort of applied force:
Individually, the first wave is propagating entirely to the right; the second wave spreads out in both directions from the point of application. What does the situation look like when both waves are applied to the string at the same time? We have:
There is complete destructive interference to the right of the second excitation. Looking at the picture, though, the actual physical result of our two excitations is that the first wave, propagating to the right, is reflected back to the left!
The proper interpretation is that the second excitation in the center of the string actually adds no energy to the string at all! In fact, the second excitation on the string just blocks and reflects the first wave. There is no “energy cancellation” involved.
Waves in a one-dimensional problem like a vibrating string are a bit of a special case; however, a similar argument can be made for higher-dimensional problems. In general, we can say that the interference of waves doesn’t “cancel” energy, it just moves it somewhere else.
The perfect illustration of this is Young’s double slit experiment, which I have discussed before:
Light emanating from the two slits in the screen A produces an interference pattern on the measurement screen B, a simulation of which is shown below:
The presence of interference means that more light shows up in some places and less light shows up in other places. It can be shown, however, using some straightforward mathematics, that the total light collected on the measurement screen B is equal to the total light that passes through the two holes: interference affects where the light goes, but not how much of it there is in total.
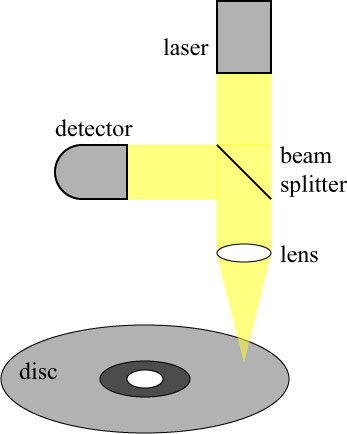
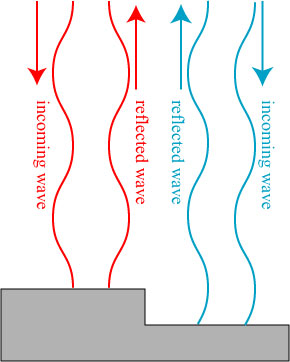
This observation — that interference redirects light, and doesn’t cancel it — actually plays a role in the operation of compact disc players. The data on a compact disc is encoded in a series of ‘pits’ surrounded by ‘land’, which correspond to a ‘0’ or ‘1’ bit. The disc is read by focusing light onto the surface, and measuring the amount of light reflected back, as crudely illustrated below:
Light from a laser passes through a beam splitter and is focused by a lens onto the disc. Part of the back-reflected light gets directed by the splitter to the detector, and the absence or presence of light at the detector registers as a ‘1’ bit or ‘0’ bit.
The modulation of light is caused by interference. Light illuminating ‘land’ gets directly reflected and collected at the detector. When a ‘pit’ is present, however, the focused beam partly reflects from land and partly from pit. If the pit is taken to be a quarter-wavelength in depth, then the light reflected from the pit is half-a-wavelength out of phase with the light from the land, resulting in destructive interference and less light at the detector:
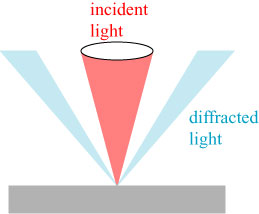
But, as noted, the light doesn’t get “canceled” completely; it just goes somewhere else. Where does it go? It gets diffracted into a direction where the lens cannot detect it (color coded for clarity):
To summarize, these are the two thoughts I had when the student asked me his question: (1) one needs to consider all sources of waves when trying to interpret wave interference phenomena, and (2) in general, wave interference results in a change in where light goes.
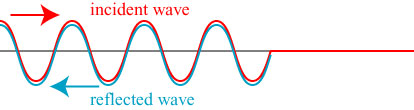
Even with this in mind, it is easy to come up with circumstances that can really challenge one’s understanding of interference. For instance, let us return to our waves on a string, and consider interference between waves generated by two local excitations:
What do we make of this situation? We have two excitations, oscillating in sync but with a half-wavelength separating them. There is destructive interference of the waves on either side of the two excitations, and the string vibrates up and down between the two excitations.
Such a strange string vibration is now known as a nonpropagating excitation, and the first research on such effects was done by my collaborators and I*! Nonpropagating excitations are actually one-dimensional analogues of the radiationless “invisible” objects that I have discussed previously (here and here, for instance).
I still haven’t come up with a great way to explain what is going on here. Let us imagine that we start applying our excitations with the string at rest. Energy goes into generating the nonpropagating excitation and some transient waves that propagate away after a short period of time. When the transients are gone, however, no more energy is added to the system. Just like the case discussed at the beginning of the post, excitation 2 serves only to reflect waves traveling from the left, and excitation 1 serves only to reflect waves traveling from the right. The two sources are playing a sort of “wave ping-pong”, knocking the waves back and forth between them! Beyond that odd statement, it is difficult to describe the exact origin of the waves without specifying the physical mechanism used to excite the string.
So, there’s no disappearance of energy in wave interference, but that doesn’t mean that interference isn’t a really weird phenomenon!
*****************************************
* My first paper on the subject is M. Berry, J.T. Foley, G. Gbur and E. Wolf, “Nonpropagating string excitations”, Am. J. Phys. 66(2) (1998), 121. It is one of my favorite papers because of the weirdness and elegance of the subject, and also because it is probably the only time I’ll have two world-renowned brilliant physicists — Emil Wolf and Michael Berry — as coauthors on the same paper. The nonpropagating excitation described in the paper is more complicated than the two point source case described here; that example was suggested by B. Denardo, “A simple explanation of simple nonradiating sources in one dimension,” Am. J. Phys. 66 (11) (1998), 1020.





Great post! I remember wondering about a similar question during my waves class. I wanted to consider something like your first picture, where two waves, each with energy, add up to nothing. Instead of thinking about sources, I imagined the waves were simply traveling down a dispersionless string from opposite directions. In that case when the waves destructively interfere the amplitude is zero everywhere, but the string is in motion. The energy is entirely kinetic.
We could also imagine two electromagnetic waves with the same frequency propagating towards each other from opposite directions in a vacuum. In that case, the electromagnetic fields could momentarily cancel, and there would be no kinetic energy around. But if the electromagnetic fields were canceling, the magnetic fields should constructively interfere.
I am going to have to dig out my EM textbook to see what we can say about energy conservation working directly from Maxwell’s equation.
I normally enjoy Am.J.Phys articles, but I’m no longer at a university. Is there a place I can read a copy of your paper?
Glad you like the post!
Send me an email, and I’ll send you the relevant pdfs directly!
Glad you like the post!
Send me an email, and I’ll send you the relevant pdfs directly!
Would it help to think about these interference questions the same way we think about real waves in physical media?
The ideal string that we derive these textbook wave examples from has internal “strain energy” due to tension and compression, similar to pressure energy in air. If you looked at the strain energy before wave cancellation, you’d see wave patterns travelling along the string, just like pressure waves travelling in air. I assume that after wave cancellation, the strain energy would be constant everywhere in the string, but at a higher value that conserves overall energy.
So with a change of wave medium from string to air, the nonpropagating excitation case could be thought of as two in-phase loudspeakers aimed at each other, but positioned a half-wavelength apart. They’d create a time-varying pressure between them, and silence (albeit with increased static pressure) everywhere else.
If you increased the distance between the speakers to a whole wavelength, I guess you’d see the opposite — silence with higher pressure between the speakers, and sound everywhere else.
But in a physical system like this, it seems like there is still energy flowing out of the sources over time, driving the increase in static pressure which is silently propagating out into the environment.
I’m currently researching ultrasonic guided waves for the non-destructive testing of engineering structures with particular interest in array design for wave mode isolation and directional transduction. I gave a workshop on manipulating superposition last week and I really wish I’d seen this post in time to bring it up in the class. Unfortunately, I’ve only just found it now, but nevertheless I will be forwarding it on to all of the attendees for them to consider.
Thanks for producing it!
You’re welcome; I’m glad you found the post useful!
thank you for sharing your thinking time with us. this post is SO helpful.
thank you that was helpful, i found this post when i was thinking about this:
2 electromagnetic radiations (plane but not infinitely) long in opposite directions and at one instant they completely destroy each other, the same thing on a standing wave when the field is all zero at one instant, where did it go,, for example on a string there is still kinetic energy without potential energy but for EM-radiation where is the energy?
Great.
When I was in the junior high school, I learned that attaching a special membrane in glasses will let more light pass through the glasses other than reflect back.
But I did’t know why, and felt quite curious how lights can “cancel” each other.
Now, I understand much more.
Thanks!
I’m glad it helped!
I am not a scientist, just a interested person. Are you saying energy can not be cancelled, it can only be deflected? In the case of a auto air-bag, it mainly deflects the energy created in a accident?
Thanks, Dwight
That is, in essence, what I’m saying, though strictly speaking we never speak of energy being “deflected”.
The auto air-bag is a somewhat different case from the waves that I’m talking about in this post, but in the collision of a person with an air-bag, the energy of motion is converted into heat & motion of the air & bag. Energy, as far as we know, is never cancelled; it gets converted into another form. Or, as in the case of the waves I mention here, stays in the same form but ends up being redistributed/redirected.
Please explain the lost energy/ energy gained during interference of sound waves.
e.g., during destructive intrfrnce, intensity of 2I becomes 0. what happens to this lost sound intensity ?
Or, in constructive intrfrnc, 2I is converted in 4I. From where does this extra 2I come from ?
This was, in essence, what I was trying to describe in this post! Energy is not, as a whole, lost or gained in the interference process — it is relocated. To use your terminology, the energy that results in 4I intensity at the constructive interference areas essentially comes from the areas where energy “disappeared’ due to destructive interference.
My question is (I think) the same as Salem’s. If two beams of monochromatic light could be directed by lenses and perfectly superimposed but out of phase so they cancel each other, what happens to their photons & their energy? Would a target detector detect anything? This seems different from the string example.
Bump for David’s question. Also in your example of the double slit experiment; I don’t think the bright parts of the interference pattern will make up for the dark spots as you suggest. The bright parts where the two light sources are constructive would have 2x the luminosity that either slit alone would shine on wall. This is the luminosity you would expect to cover the entire wall if interference did not occur. However interference causes part of the wall to have dark stripes. Where did that energy (of the light that would have hit the wall assuming no interference) go!? If your statement that the energy from the destructive wave parts is moved to the constructive part was true then you would expect 4x the luminosity on the bright stripes but that is not what happens! I don’t understand your explanation; could you plz elaborate on where that energy went.
Ok I am wrong because the luminosity in the bright bands being only 2x because the energy of a light wave is actually 4x (the amplitude squared). So this is my guess about where the energy goes when creating a wave which completely constructs or destructs another one. In the case of creating a wave w2 which interferes constructively with another wave w1 (assume both w2 & w1 have the same amplitude so the resulting net wave will have 4x the energy). It will require 3x the energy to generate wave w2 as was previously needed to generate wave w1. In the case of creating a wave w2 which interferes destructively with another wave w1. All the energy of the wave w1 will lost in the device that is generating w2 since it is essentially resisting the wave w1? I don’t think my scenario could work if the waves are generated moving towards each other instead of in the same direction so I have no clue how that would work out. In the case of constructive interference you would have a wave with 2x the amplitude = 4x the energy where the waves overlap. Where does that doubling energy come from (you start with two waves each with x energy = 2x but end up with 1 superimposed wave with 4x energy)? Does it matter that the waves are traveling in the opposite direction?
In fact, in Young’s experiment one can show rigorously that the total energy of the interfered waves is exactly the energy being emitted by the two slits; the energy in this case is in fact being “redirected”.
In terms of the complete interference of two waves, my post gives the best explanation I can present: in such a case, one has to look back at the sources of the waves. When this is done, the “cancellation” can usually be interpreted in terms of reflection.
I would be interested in taking a look at the mathematics behind the proof for conservation of energy in the double slit experiment, could you point me at some material where this is shown?
Thanks in advance.
I don’t think I’ve seen a formal proof of conservation of energy — the approximations used in deriving the “standard” formulas for the double slit experiment make a formal proof rather “iffy”.
A simple argument is as follows: in the middle of the measurement screen, the intensity of light from each of the pinholes is more or less uniform and equal. We say that the intensity is I0 for each contribution, meaning that the total intensity (without interference) that would be seen on the screen as a function of x would be I(x) = 2I0.
With interference, the intensity on the screen is, according to the conventional formulas for the double slit, I(x) = 2I0 + 2I0 sin(kx), where k is the wavenumber of light. Because of the sine function, the intensity is higher for some x values, and lower for others. If we look at the total energy over a single period of the interference pattern, i.e. we integrate I(x) over x from 0 to 2 Pi/k, the sine contribution vanishes and we are left with 4Pi I0/k. This is exactly the result we would get from integrating the interference-free intensity I(x) =2I0 over the same period.
Things are a bit more complicated with the complete interference pattern, because the overall spot is brightest in the middle, and fades to zero at the edges. There are also polarization effects to take into account, and the integral can be quite messy.
Nevertheless, in any local region the math indicates that interference simply “reorganizes” the energy, and that none of it disappears.
The redirection of energy during interference is a contentious, though reasonable issue.
Opponents of redirection cite Feynman’s rule of non-interaction of photons and Dirac’s assertion of photon non-interaction. In a wikipedia article that mentioned redirection of energy during interference; The redirection statement was withdrawn and relegated to the discussion section under a cloud of doubt. Before I attempt to publish data diagrams and photographs supporting redirection and its odd mechanism, what support do you use to overcome the non-interaction dogma?
I was using the word “redirection” in a very loose sense, and didn’t intend to imply any deeper philosophical issue (presumably regarding momentum of photons).
I use the term “redirection” simply to point out that interference doesn’t cause the “destruction” of energy; the total power in an interference pattern is equal to the total power of the individual interfering fields. Dark spots in an interference pattern are balanced by the bright spots.
Dirac’s photon non-interaction statement is itself much less of a clear statement than most people appreciate, nevertheless; I talk about it somewhat here.
Thank you for referring to your non-interaction of photons article. A paper by J. P. Dowling and J. Gea-Banacloche, “The specular reflection of light off light,” Am. J. Phys. 60, 28-34 (1992) opened with an apologetic tone that their proposal was not consistent with the non-interaction rule. Their publication, though very carefully reasoned, has been cited only once. Like so many physics 101 students in 1960, I found discussions of light interference confounding. With generous guidance from a physicist friend and collaborator I set up a minimal lab to examine how light moves during interference. The only publication consistent with the results was the “specular reflection” paper.
Now the results are extending into new domains. But, the non-interaction rule has my collaborator and his advisors balking. Perhaps your rebuttal and subsequent comments, that have been forwarded, will change minds.
Thanks buddy… teachers like u r great
Your first explanation is wrong. Because you only assumed only second string has dual propagation. If you consider the first string is also dual propagating in left and right at the same time, you would only get a standing wave in the center region between two sources. Eventually, you are putting power to create 2 equal amplitude waves and only get a power equal to one wave oscillates back and forth creating standing wave. Then you already lost the power that can create one wave.
Furthermore, if you make the two source that make wave in both directions, you will end up with complete destructive interference. So, we are back to the question again.
typo on above comment ” If you make the distances between two sources zero,”
above post was quite wonderful and i like the way you have explained the concept , my question is that we know that during interference energy is relocated but how, suppose we have two pressure waves(sound) which are travelling in opposite direction and having same amplitude then at any point in air where destructive interference occur net displacement in air molecule will be zero since both the waves are in opposite direction then what makes the next particles in motion. there are a lot of people who suggested that there are two parameters which defines the presence of pressure wave in any medium first is change in pressure and second is velocity of particles of medium, if net pressure becomes zero then the velocities will add up and if velocities become zero then change in pressure will add up, help me to understand this concept and also give me your valuable suggestion. also if you agree with this two variable concept than is there any mathematical proof for this theory. thank you very much
If you have two identical loudspeakers playing the same sound but wired out of phase, there will be a spot equidistant from them both where the sound disappears. Where does it go? I’d say that the pressure wave rises but the displacement wave drops to zero and since we only hear displacement, we hear no sound.
well i think that was a better explanation , but still i do want to know what exactly we mean that “we only hear displacement” not pressure, i think our ears have drums which sends signals to brain whenever pressure is applied over them
Hi himanshu,
Only displacement moves your eardrum. Pressure does not. So we only hear displacement. But power equals pressure times displacement and the phase angle between them.
Bob
It was very interesting!!!!!!…but I feel little comfused and I want to ask you about something.At the image with the red incoming wave and the reflected one….why the blue reflected wave don’t have a 180 degree phase difference withe the blue incoming wave???
Energy is in Space (medium). Think of a string, one person jerks upward from left, one person jerks downward from the right. When the two peak meet, they cancel out. Where’s the energy when they are canceled out? In the string’s tensions. Of course the more interesting question is what is tension of time space.